The Free Particle

TL;DR

• Free particle: $V(x)=0$, no boundary conditions (arbitrary energy)
• The separated solution $\Psi_k(x,t) = Ae^{i\left(kx-\frac{\hbar k^2}{2m}t \right)}$ diverges to infinity when square-integrated and cannot be normalized, which implies:
  • Free particles cannot exist as stationary states
  • Free particles cannot have energy defined as a single precise value (energy uncertainty exists)
• Nevertheless, since the general solution of the time-dependent Schrödinger equation is a linear combination of separated solutions, the separated solution still has important mathematical significance. However, in this case, since there are no constraints, the general solution takes the form of an integral ($\int$) over the continuous variable $k$ rather than a sum ($\sum$) over the discrete variable $n$.
• General solution of the Schrödinger equation:

\[\begin{gather*} \Psi(x,t) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \phi(k)e^{i(kx-\frac{\hbar k^2}{2m}t)}dk, \\ \text{where }\phi(k) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\Psi(x,0)e^{-ikx}dx \end{gather*}\]

• Relationship between position uncertainty and momentum uncertainty:
  • When position uncertainty decreases, momentum uncertainty increases, and conversely, when momentum uncertainty decreases, position uncertainty increases
  • That is, it is impossible to know both the position and momentum of a free particle precisely at the same time quantum mechanically
• Phase velocity and group velocity of the wave function $\Psi(x,t)$:
  • Phase velocity: $v_\text{phase} = \cfrac{\omega}{k} = \cfrac{\hbar k}{2m}$
  • Group velocity: $v_\text{group} = \cfrac{d\omega}{dk} = \cfrac{\hbar k}{m}$
• Physical meaning of group velocity and comparison with classical mechanics:
  • Physically, the group velocity represents the velocity of motion of the particle
  • When $\phi(k)$ has a very sharp form near some value $k_0$ (when momentum uncertainty is sufficiently small),

\[v_\text{group} = v_\text{classical} = \sqrt{\cfrac{2E}{m}}\]

Prerequisites

• Euler’s formula
• Fourier transform & Plancherel’s theorem
• Schrödinger Equation and the Wave Function
• Time-Independent Schrödinger Equation
• The 1D Infinite Square Well

Model Setup

Let’s examine the simplest case of a free particle ($V(x)=0$). Classically, this is simply uniform motion, but in quantum mechanics this problem is more interesting.
The time-independent Schrödinger equation for a free particle is

\[-\frac{\hbar^2}{2m}\frac{d^2\psi}{dx^2}=E\psi \tag{1}\]

that is

\[\frac{d^2\psi}{dx^2} = -k^2\psi \text{, where }k\equiv \frac{\sqrt{2mE}}{\hbar} \label{eqn:t_independent_schrodinger_eqn}\tag{2}\]

Up to this point, it’s the same as inside an infinite square well with potential $0$. However, this time let’s write the general solution in the following exponential form.

\[\psi(x) = Ae^{ikx} + Be^{-ikx}. \tag{3}\]

$Ae^{ikx} + Be^{-ikx}$ and $C\cos{kx}+D\sin{kx}$ are equivalent ways of writing the same function of $x$. By Euler’s formula $e^{ix}=\cos{x}+i\sin{x}$,

\[\begin{align*} Ae^{ikx}+Be^{-ikx} &= A[\cos{kx}+i\sin{kx}] + B[\cos{(-kx)}+i\sin{(-kx)}] \\ &= A(\cos{kx}+i\sin{kx}) + B(\cos{kx}-i\sin{kx}) \\ &= (A+B)\cos{kx} + i(A-B)\sin{kx}. \end{align*}\]

That is, setting $C=A+B$, $D=i(A-B)$, we get

\[Ae^{ikx} + Be^{-ikx} = C\cos{kx}+D\sin{kx}. \blacksquare\]

Conversely, expressing $A$ and $B$ in terms of $C$ and $D$, we get $A=\cfrac{C-iD}{2}$, $B=\cfrac{C+iD}{2}$.

In quantum mechanics, when $V=0$, exponential functions represent traveling waves and are most convenient when dealing with free particles. On the other hand, sine and cosine functions are suitable for representing standing waves and naturally appear in the case of infinite square wells.

Unlike the infinite square well, this time there are no boundary conditions that constrain $k$ and $E$. That is, a free particle can have any positive energy.

Separated Solution and Phase Velocity

Adding the time dependence $e^{-iEt/\hbar}$ to $\psi(x)$, we get

\[\Psi(x,t) = Ae^{ik\left(x-\frac{\hbar k}{2m}t \right)} + Be^{-ik\left(x+\frac{\hbar k}{2m}t \right)} \label{eqn:Psi_seperated_solution}\tag{4}\]

Any function of $x$ and $t$ that depends on the special form $(x\pm vt)$ represents a wave that moves in the $\mp x$ direction at speed $v$ without changing shape. Therefore, the first term in equation ($\ref{eqn:Psi_seperated_solution}$) represents a wave moving to the right, and the second term represents a wave with the same wavelength and propagation speed but different amplitude moving to the left. Since they differ only in the sign in front of $k$, we can write

\[\Psi_k(x,t) = Ae^{i\left(kx-\frac{\hbar k^2}{2m}t \right)} \tag{5}\]

where the direction of wave propagation according to the sign of $k$ is as follows.

\[k \equiv \pm\frac{\sqrt{2mE}}{\hbar},\quad \begin{cases} k>0 \Rightarrow & \text{moving to the right}, \\ k<0 \Rightarrow & \text{moving to the left}. \end{cases} \tag{6}\]

The ‘stationary state’ of a free particle is clearly a traveling wave*, with wavelength $\lambda = 2\pi/|k|$ and momentum given by the de Broglie formula

\[p = \frac{2\pi\hbar}{\lambda} = \hbar k \label{eqn:de_broglie_formula}\tag{7}\]

*A ‘stationary state’ being a traveling wave is obviously physically contradictory. The reason will become clear shortly.

Also, the speed of this wave is as follows.

\[v_{\text{phase}} = \left|\frac{\omega}{k}\right| = \frac{\hbar|k|}{2m} = \sqrt{\frac{E}{2m}}. \label{eqn:phase_velocity}\tag{8}\]

(Here $\omega$ is the coefficient $\cfrac{\hbar k^2}{2m}$ in front of $t$.)

However, this wave function diverges to infinity when square-integrated and cannot be normalized.

\[\int_{-\infty}^{\infty}\Psi_k^*\Psi_k dx = |A|^2\int_{-\infty}^{\infty}dx = \infty. \tag{9}\]

That is, for free particles, the separated solution is not a physically possible state. Free particles cannot exist as stationary states, nor can they have any specific energy value. In fact, intuitively, it would be stranger for standing waves to form when there are no boundary conditions at either end.

Finding the General Solution $\Psi(x,t)$ of the Time-Dependent Schrödinger Equation

Nevertheless, this separated solution still has important meaning because, regardless of physical interpretation, the general solution of the time-dependent Schrödinger equation is a linear combination of separated solutions, which has mathematical significance. However, since there are no constraints in this case, the general solution takes the form of an integral ($\int$) over the continuous variable $k$ instead of a sum ($\sum$) over the discrete variable $n$.

\[\Psi(x,t) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \phi(k)e^{i(kx-\frac{\hbar k^2}{2m}t)}dk. \label{eqn:Psi_general_solution}\tag{10}\]

Here, $\cfrac{1}{\sqrt{2\pi}}\phi(k)dk$ plays the same role as $c_n$ in equation (21) of the ‘Time-Independent Schrödinger Equation’ post.

This wave function can be normalized for appropriate $\phi(k)$, but it must have a range of $k$ and therefore a range of energy and speed. This is called a wave packet.

Sine functions are infinitely spread in space and cannot be normalized. However, when multiple such waves are superposed, they become localized and normalizable due to interference.

Finding $\phi(k)$ Using Plancherel’s Theorem

Now that we know the form of $\Psi(x,t)$ (equation [$\ref{eqn:Psi_general_solution}$]), we just need to determine $\phi(k)$ that satisfies the initial wave function

\[\Psi(x,0) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \phi(k)e^{ikx}dk \label{eqn:Psi_at_t_0}\tag{11}\]

This is a typical problem in Fourier analysis, and the answer can be obtained using Plancherel’s theorem.

\[f(x) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} F(k)e^{ikx}dk \Longleftrightarrow F(k)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}f(x)e^{-ikx}dx. \label{eqn:plancherel_theorem}\tag{12}\]

$F(k)$ is called the Fourier transform of $f(x)$, and $f(x)$ is called the inverse Fourier transform of $F(k)$. From equation ($\ref{eqn:plancherel_theorem}$), we can easily see that the only difference between them is the sign of the exponent. Of course, there is a constraint that only functions for which the integral exists are allowed.

The necessary and sufficient condition for $f(x)$ to exist is that $\int_{-\infty}^{\infty}|f(x)|^2dx$ must be finite. In this case, $\int_{-\infty}^{\infty}|F(k)|^2dk$ is also finite, and

\[\int_{-\infty}^{\infty}|f(x)|^2 dx = \int_{-\infty}^{\infty}|F(k)|^2 dk\]

Some people refer to the above equation as Plancherel’s theorem rather than equation ($\ref{eqn:plancherel_theorem}$) (Wikipedia also describes it this way).

In our current case, the integral necessarily exists due to the physical condition that $\Psi(x,0)$ must be normalized. Therefore, the quantum mechanical solution for a free particle is equation ($\ref{eqn:Psi_general_solution}$), where

\[\phi(k) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\Psi(x,0)e^{-ikx}dx \label{eqn:phi}\tag{13}\]

However, in practice, the integral in equation ($\ref{eqn:Psi_general_solution}$) can rarely be solved analytically. Usually, values are obtained using numerical analysis with computers.

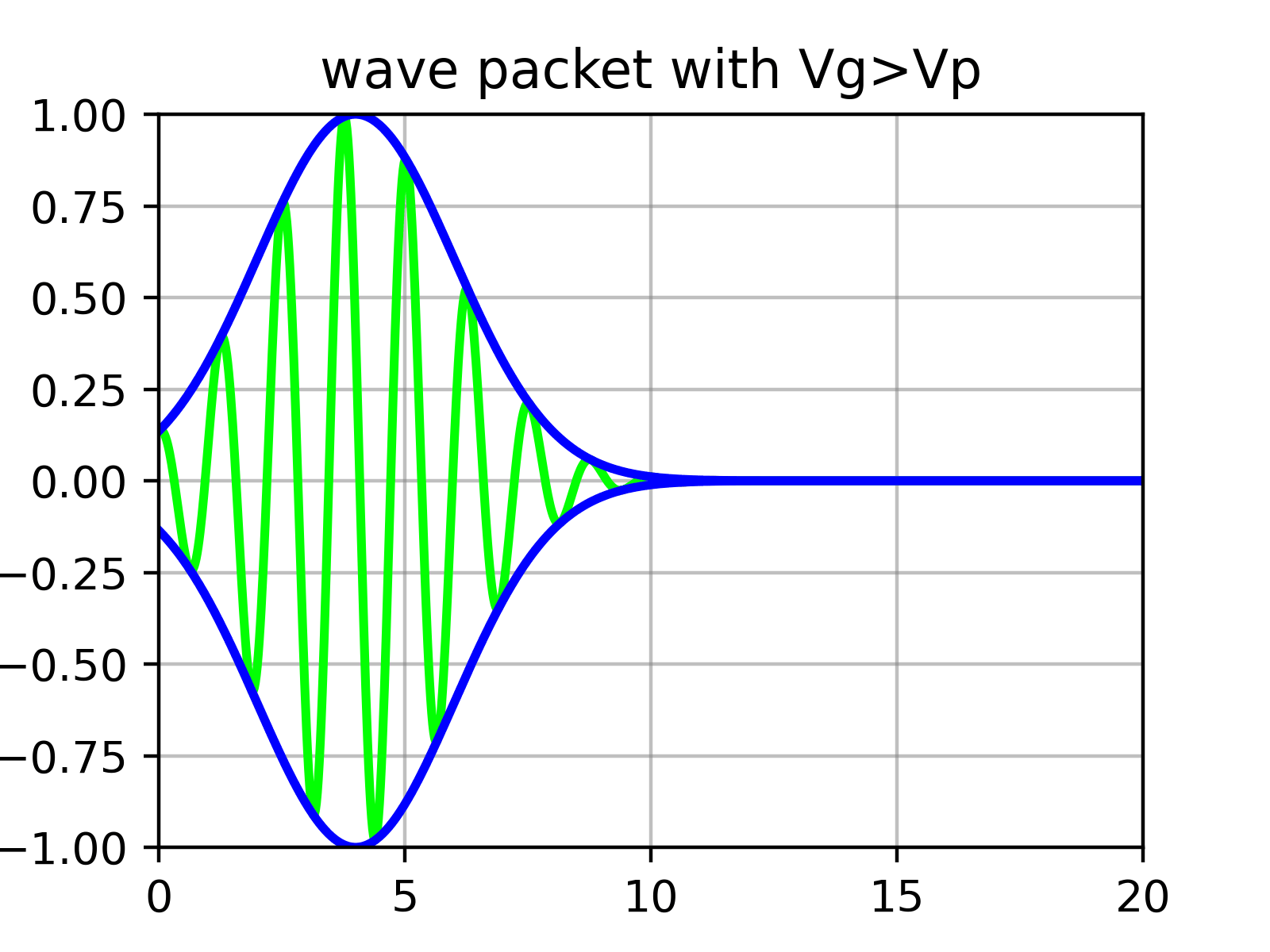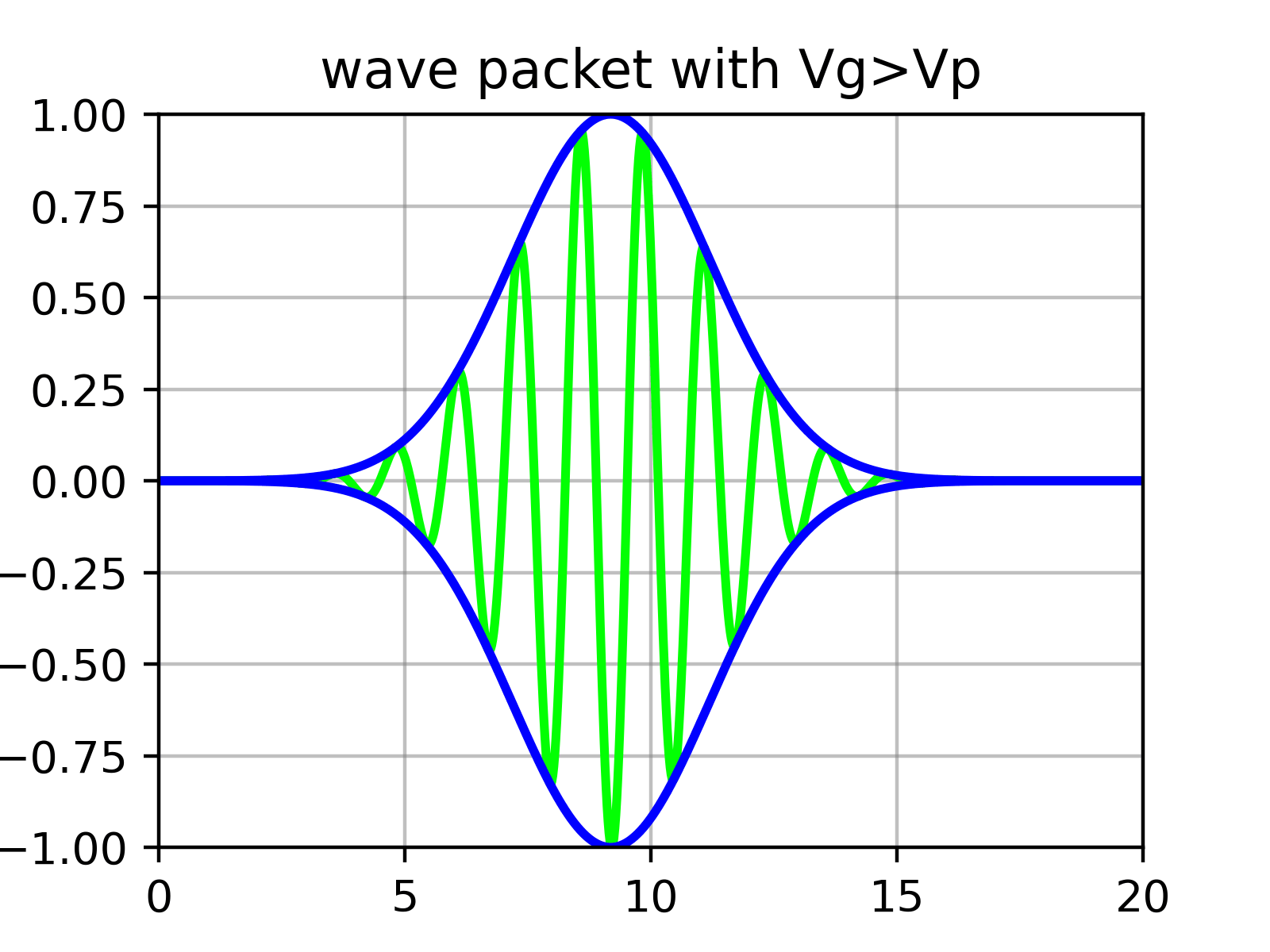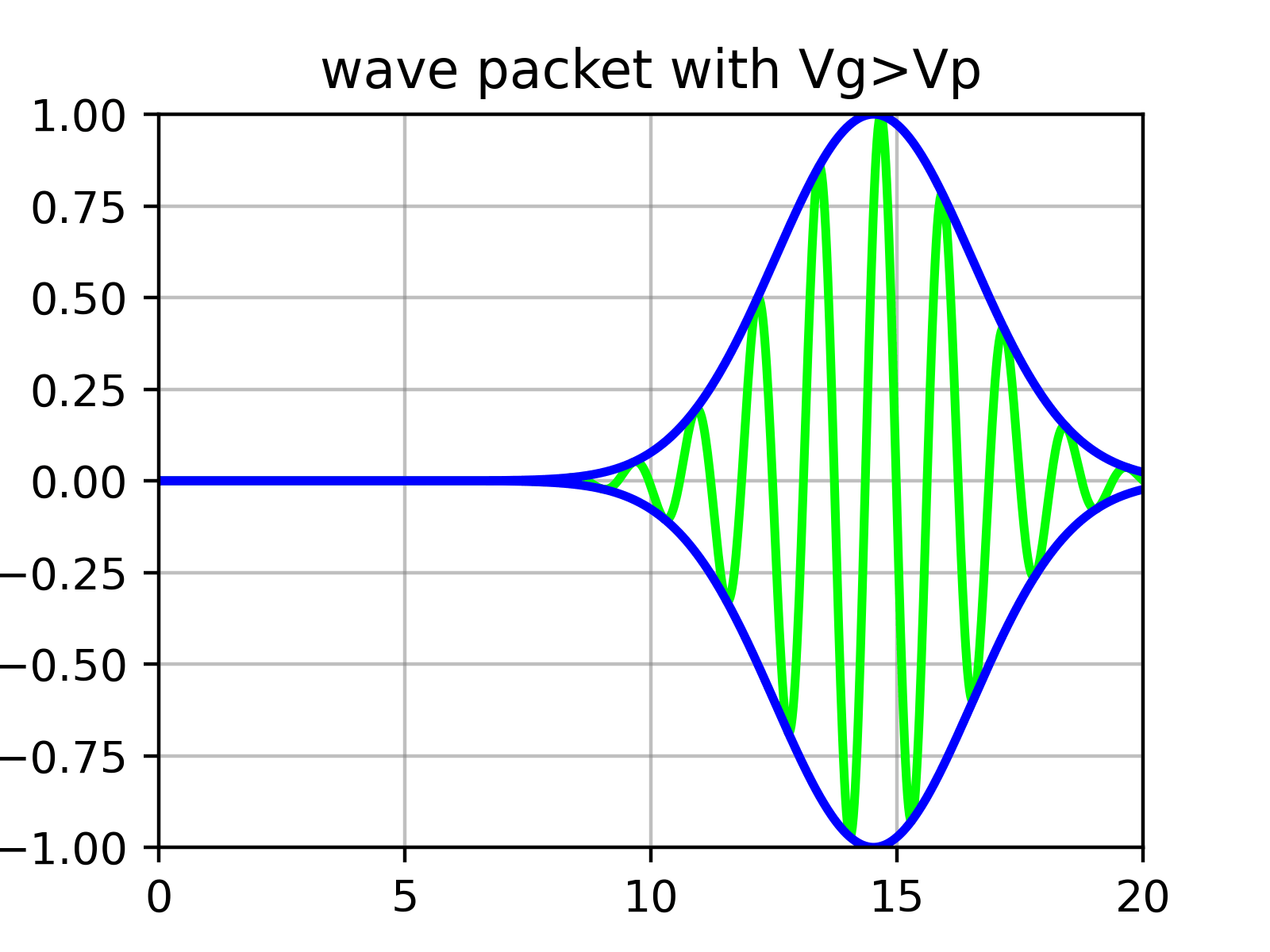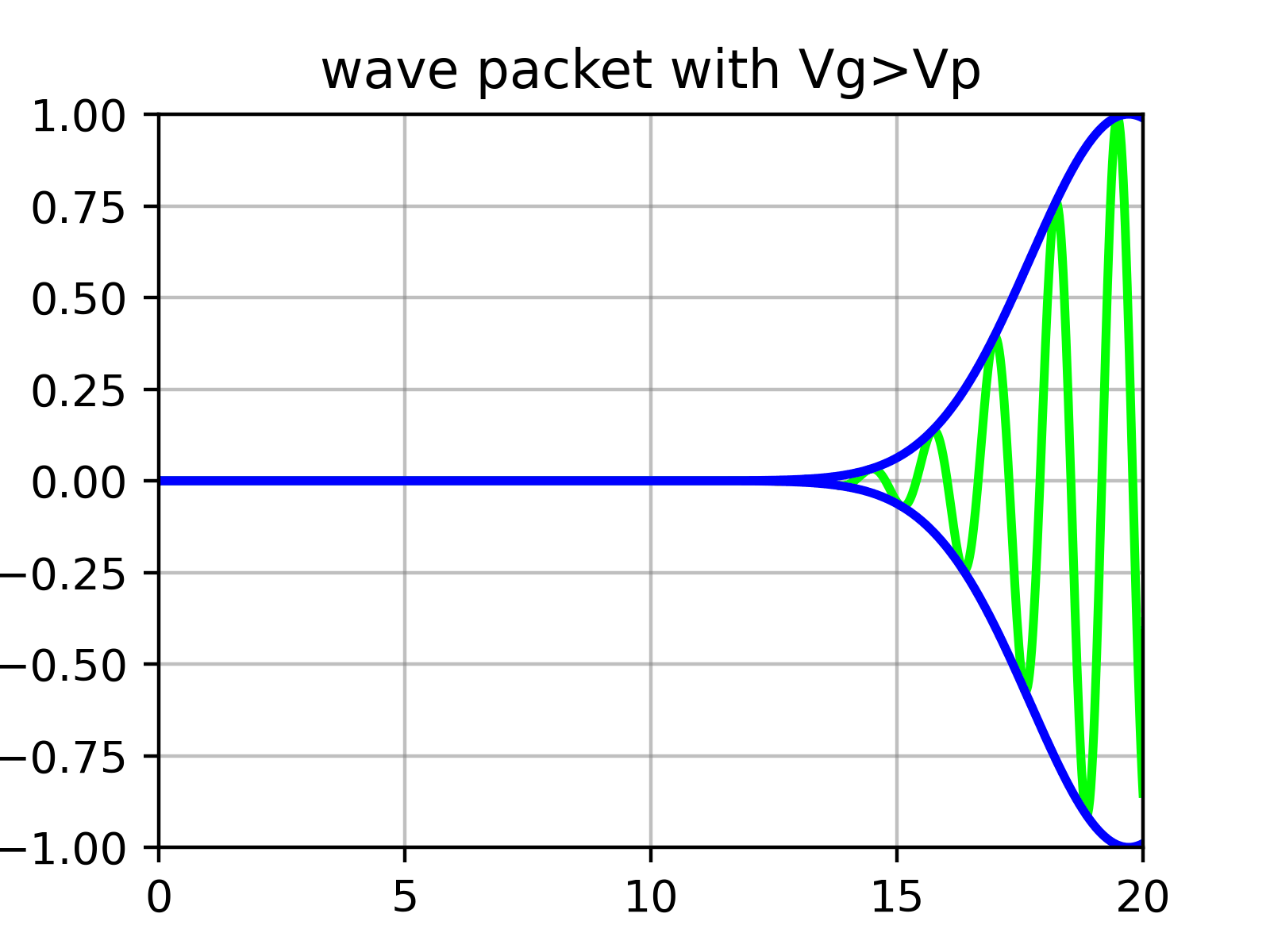
Calculating the Group Velocity of Wave Packets and Physical Interpretation

Essentially, a wave packet is a superposition of numerous sine functions whose amplitudes are determined by $\phi$. That is, there are ‘ripples’ within the ‘envelope’ that forms the wave packet.

Image license and source attribution

• Image generation source code (gnuplot): yunseo-kim/physics-visualizations
• License: Mozilla Public License 2.0
• Original author: Ph.D. Youjun Hu
• Original license notice: MIT License

What physically corresponds to the particle’s velocity is not the velocity of individual ripples (phase velocity) calculated in equation ($\ref{eqn:phase_velocity}$), but the velocity of the outer envelope (group velocity).

Relationship Between Position Uncertainty and Momentum Uncertainty

Let’s examine the relationship between position uncertainty and momentum uncertainty by separately considering the integrand parts $\int\phi(k)e^{ikx}dk$ in equation ($\ref{eqn:Psi_at_t_0}$) and $\int\Psi(x,0)e^{-ikx}dx$ in equation ($\ref{eqn:phi}$).

When position uncertainty is small

When $\Psi$ in position space is distributed in a very narrow region $[x_0-\delta, x_0+\delta]$ around some value $x_0$ and is close to 0 outside this region (when position uncertainty is small), $e^{-ikx} \approx e^{-ikx_0}$ is nearly constant with respect to $x$, so

\[\begin{align*} \int_{-\infty}^{\infty} \Psi(x,0)e^{-ikx}dx &\approx \int_{x_0-\delta}^{x_0+\delta} \Psi(x,0)e^{-ikx_0}dx \\ &= e^{-ikx_0}\int_{x_0-\delta}^{x_0+\delta} \Psi(x,0)dx \\ &= e^{-ipx_0/\hbar}\int_{x_0-\delta}^{x_0+\delta} \Psi(x,0)dx \quad (\because \text{eqn. }\ref{eqn:de_broglie_formula}) \end{align*}\tag{14}\]

Since the definite integral term is constant with respect to $p$, the preceding $e^{-ipx_0/\hbar}$ term causes $\phi$ to have a sinusoidal form with respect to $p$ in momentum space, meaning it is distributed over a wide momentum range (momentum uncertainty is large).

When momentum uncertainty is small

Similarly, when $\phi$ in momentum space is distributed in a very narrow region $[p_0-\delta, p_0+\delta]$ around some value $p_0$ and is close to 0 outside this region (when momentum uncertainty is small), by equation ($\ref{eqn:de_broglie_formula}$), $e^{ikx}=e^{ipx/\hbar} \approx e^{ip_0x/\hbar}$ is nearly constant with respect to $p$ and $dk=\frac{1}{\hbar}dp$, so

\[\begin{align*} \int_{-\infty}^{\infty} \phi(k)e^{ikx}dk &= \frac{1}{\hbar}\int_{p_0-\delta}^{p_0+\delta} \phi(p)e^{ip_0x/\hbar}dp \\ &= \frac{1}{\hbar}e^{ip_0x/\hbar}\int_{p_0-\delta}^{p_0+\delta} \phi(p)dp \end{align*}\tag{15}\]

The preceding $e^{ip_0x/\hbar}$ term causes $\Psi$ to have a sinusoidal form with respect to $x$ in position space, meaning it is distributed over a wide position range (position uncertainty is large).

Conclusion

When position uncertainty decreases, momentum uncertainty increases, and conversely, when momentum uncertainty decreases, position uncertainty increases. Therefore, it is impossible to know both the position and momentum of a free particle precisely at the same time quantum mechanically.

Image source

• Author: English Wikipedia user Maschen
• License: public domain

In fact, by the uncertainty principle, this applies not only to free particles but to all cases. The uncertainty principle will be covered in a separate post later.

Group Velocity of Wave Packets

Rewriting the general solution in equation ($\ref{eqn:Psi_general_solution}$) with $\omega \equiv \cfrac{\hbar k^2}{2m}$ as in equation ($\ref{eqn:phase_velocity}$), we get

\[\Psi(x,t) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \phi(k)e^{i(kx-\omega t)}dk \tag{16}\]

An equation expressing $\omega$ as a function of $k$, such as $\omega = \cfrac{\hbar k^2}{2m}$, is called a dispersion relation. The content that follows applies generally to all wave packets regardless of the dispersion relation.

Now assume that $\phi(k)$ has a very sharp form near some appropriate value $k_0$. (It’s fine if it’s spread widely over $k$, but such wave packets change shape very quickly and become different forms. Since components for different $k$ move at different speeds, they lose the meaning of a well-defined ‘group’ with velocity. That is, momentum uncertainty increases.)
Since the integrand can be neglected except near $k_0$, we can Taylor expand the function $\omega(k)$ near this point, and keeping only up to the first-order term, we get

\[\omega(k) \approx \omega_0 + \omega_0^\prime(k-k_0)\]

Now substituting $s=k-k_0$ and integrating centered on $k_0$, we get

\[\begin{align*} \Psi(x,t) &= \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\phi(k_0+s)e^{i[(k_0+s)x-(\omega_0+\omega_0^\prime s)t]}ds \\ &= \frac{1}{\sqrt{2\pi}}e^{i(k_0x-\omega_0t)}\int_{-\infty}^{\infty}\phi(k_0+s)e^{is(x-\omega_0^\prime t)}ds. \end{align*}\tag{17}\]

The term in front, $e^{i(k_0x-\omega_0t)}$, represents a sine wave (‘ripples’) moving at speed $\omega_0/k_0$, and the integral term (‘envelope’) that determines the amplitude of this sine wave moves at speed $\omega_0^\prime$ due to the $e^{is(x-\omega_0^\prime t)}$ part. Therefore, the phase velocity at $k=k_0$ is

\[v_\text{phase} = \frac{\omega_0}{k_0} = \frac{\omega}{k} = \frac{\hbar k}{2m} \tag{18}\]

which confirms again that it equals the value in equation ($\ref{eqn:phase_velocity}$), and the group velocity is

\[v_\text{group} = \omega_0^\prime = \frac{d\omega}{dk} = \frac{\hbar k}{m} \label{eqn:group_velocity}\tag{19}\]

which is twice the phase velocity.

Comparison with Classical Mechanics

Since we know that classical mechanics holds at macroscopic scales, the results obtained through quantum mechanics should be able to approximate the calculation results from classical mechanics when quantum uncertainties are sufficiently small. In the case of the free particle we’re dealing with, when $\phi(k)$ has a very sharp form near some appropriate value $k_0$ as assumed earlier (i.e., when momentum uncertainty is sufficiently small), the group velocity $v_\text{group}$ corresponding to the particle’s speed in quantum mechanics should equal the particle’s speed $v_\text{classical}$ obtained from classical mechanics for the same $k$ and corresponding energy value $E$.

Substituting $k\equiv \cfrac{\sqrt{2mE}}{\hbar}$ from equation ($\ref{eqn:t_independent_schrodinger_eqn}$) into the group velocity (equation [$\ref{eqn:group_velocity}$]) we just found, we get

\[v_\text{quantum} = \sqrt{\frac{2E}{m}} \tag{20}\]

and the speed of a free particle with kinetic energy $E$ in classical mechanics is likewise

\[v_\text{classical} = \sqrt{\frac{2E}{m}} \tag{21}\]

Therefore, since $v_\text{quantum}=v_\text{classical}$, we can confirm that the result obtained by applying quantum mechanics is a physically valid solution.