Campo gravitacional y potencial gravitacional

TL;DR

• Ley de gravitación universal de Newton: $\mathbf{F} = -G\cfrac{mM}{r^2}\mathbf{e}_r$
• Para objetos con distribución continua de masa y tamaño: $\mathbf{F} = -Gm\int_V \cfrac{dM}{r^2}\mathbf{e}_r = -Gm\int_V \cfrac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2} dv^{\prime}$
  • $\rho(\mathbf{r^{\prime}})$: densidad de masa en el punto ubicado en el vector de posición $\mathbf{r^{\prime}}$ desde un origen arbitrario
  • $dv^{\prime}$: elemento de volumen en el punto ubicado en el vector de posición $\mathbf{r^{\prime}}$ desde un origen arbitrario
• Vector de campo gravitacional:
  • Vector que representa la fuerza por unidad de masa que experimenta una partícula en el campo creado por un objeto de masa $M$
  • $\mathbf{g} = \cfrac{\mathbf{F}}{m} = - G \cfrac{M}{r^2}\mathbf{e}_r = - G \int_V \cfrac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2}dv^\prime$
  • Tiene dimensiones de fuerza por unidad de masa o aceleración
• Potencial gravitacional:
  • $\mathbf{g} \equiv -\nabla \Phi$
  • Tiene dimensiones de (fuerza por unidad de masa) $\times$ (distancia) o energía por unidad de masa
  • $\Phi = -G\cfrac{M}{r}$
  • Solo las diferencias relativas del potencial gravitacional tienen significado, no valores específicos
  • Usualmente se establece la condición $\Phi \to 0$ cuando $r \to \infty$ para eliminar la ambigüedad
  • $U = m\Phi, \quad \mathbf{F} = -\nabla U$
• Potencial gravitacional dentro y fuera de una cáscara esférica (teorema de la cáscara)
  • Cuando $R>a$:
    • $\Phi(R>a) = -\cfrac{GM}{R}$
    • Al calcular el potencial gravitacional en un punto externo debido a una distribución esféricamente simétrica de materia, se puede considerar el objeto como una masa puntual
  • Cuando $R<b$:
    • $\Phi(R<b) = -2\pi\rho G(a^2 - b^2)$
    • Dentro de una cáscara de masa esféricamente simétrica, el potencial gravitacional es constante independientemente de la posición, y la gravedad actuante es $0$
  • Cuando $b<R<a$: $\Phi(b<R<a) = -4\pi\rho G \left( \cfrac{a^2}{2} - \cfrac{b^3}{3R} - \cfrac{R^2}{6} \right)$

Campo gravitacional

Ley de gravitación universal de Newton

Newton ya había sistematizado y verificado numéricamente la ley de gravitación universal antes del año 11666 HE. Sin embargo, tardó 20 años más en publicar sus resultados en su obra Principia en 11687 HE, porque no podía justificar el método de cálculo que asumía la Tierra y la Luna como masas puntuales sin tamaño. Afortunadamente, usando el cálculo que el propio Newton inventó posteriormente, podemos demostrar mucho más fácilmente ese problema que no fue sencillo para Newton en los años 1600.

Según la ley de gravitación universal de Newton, cada partícula de masa atrae a todas las demás partículas del universo con una fuerza que es proporcional al producto de las dos masas e inversamente proporcional al cuadrado de la distancia entre ellas. Matemáticamente se expresa como:

\[\mathbf{F} = -G\frac{mM}{r^2}\mathbf{e}_r \label{eqn:law_of_gravitation}\tag{1}\]

Fuente de la imagen

• Autor: Usuario de Wikimedia Dennis Nilsson
• Licencia: CC BY 3.0

El vector unitario $\mathbf{e}_r$ apunta desde $M$ hacia $m$, y el signo negativo indica que la fuerza es atractiva. Es decir, $m$ es atraída hacia $M$.

Experimento de Cavendish

La verificación experimental de esta ley y la determinación del valor de $G$ fue realizada por el físico británico Henry Cavendish en 11798 HE. El experimento de Cavendish utilizó una balanza de torsión compuesta por dos pequeñas esferas fijadas en los extremos de una barra ligera. Cada una de estas esferas es atraída hacia otras dos esferas grandes ubicadas cerca de ellas. El valor oficial de $G$ determinado hasta ahora es $6.673 \pm 0.010 \times 10^{-11} \mathrm{N\cdot m^2/kg^2}$.

Aunque $G$ es una de las constantes fundamentales conocidas desde hace más tiempo, se conoce con menor precisión que la mayoría de las otras constantes fundamentales como $e$, $c$, $\hbar$. Incluso hoy en día se realizan muchas investigaciones para determinar el valor de $G$ con mayor precisión.

Caso de objetos con tamaño

La ley de la ecuación ($\ref{eqn:law_of_gravitation}$) se aplica estrictamente solo a partículas puntuales. Si uno o ambos objetos tienen cierto tamaño, se debe hacer la suposición adicional de que el campo gravitacional es un campo lineal para calcular la fuerza. Es decir, se asume que la fuerza gravitacional total que recibe una partícula de masa $m$ de varias otras partículas se puede obtener sumando vectorialmente cada fuerza. Para objetos con distribución continua de materia, la suma se reemplaza por una integral:

\[\mathbf{F} = -Gm\int_V \frac{dM}{r^2}\mathbf{e}_r = -Gm\int_V \frac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2} dv^{\prime} \label{eqn:integral_form}\tag{2}\]

• $\rho(\mathbf{r^{\prime}})$: densidad de masa en el punto ubicado en el vector de posición $\mathbf{r^{\prime}}$ desde un origen arbitrario
• $dv^{\prime}$: elemento de volumen en el punto ubicado en el vector de posición $\mathbf{r^{\prime}}$ desde un origen arbitrario

Si tanto el objeto de masa $M$ como el objeto de masa $m$ tienen tamaño, se necesita una segunda integral de volumen sobre $m$ para obtener la fuerza gravitacional total.

Vector de campo gravitacional

El vector de campo gravitacional $\mathbf{g}$ se define como el vector que representa la fuerza por unidad de masa que experimenta una partícula en el campo creado por un objeto de masa $M$:

\[\mathbf{g} = \frac{\mathbf{F}}{m} = - G \frac{M}{r^2}\mathbf{e}_r \label{eqn:g_vector}\tag{3}\]

o

\[\boxed{\mathbf{g} = - G \int_V \frac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2}dv^\prime} \tag{4}\]

Aquí, la dirección de $\mathbf{e}_r$ varía según $\mathbf{r^\prime}$.

Esta cantidad $\mathbf{g}$ tiene dimensiones de fuerza por unidad de masa o aceleración. La magnitud del vector de campo gravitacional $\mathbf{g}$ cerca de la superficie terrestre es igual a la cantidad que llamamos constante de aceleración gravitacional, donde $|\mathbf{g}| \approx 9.80\mathrm{m/s^2}$.

Potencial gravitacional

Definición

El vector de campo gravitacional $\mathbf{g}$ varía como $1/r^2$, por lo que satisface la condición ($\nabla \times \mathbf{g} \equiv 0$) para ser expresado como el gradiente de alguna función escalar (potencial). Por lo tanto, podemos escribir:

\[\mathbf{g} \equiv -\nabla \Phi \label{eqn:gradient_phi}\tag{5}\]

donde $\Phi$ se llama potencial gravitacional y tiene dimensiones de (fuerza por unidad de masa) $\times$ (distancia) o energía por unidad de masa.

Como $\mathbf{g}$ depende solo del radio, $\Phi$ también varía con $r$. De las ecuaciones ($\ref{eqn:g_vector}$) y ($\ref{eqn:gradient_phi}$):

\[\nabla\Phi = \frac{d\Phi}{dr}\mathbf{e}_r = G\frac{M}{r^2}\mathbf{e}_r\]

Integrando esto obtenemos:

\[\boxed{\Phi = -G\frac{M}{r}} \label{eqn:g_potential}\tag{6}\]

Como solo las diferencias relativas del potencial gravitacional tienen significado y no la magnitud de los valores absolutos, podemos omitir la constante de integración. Usualmente se establece arbitrariamente la condición $\Phi \to 0$ cuando $r \to \infty$ para eliminar la ambigüedad, y la ecuación ($\ref{eqn:g_potential}$) también satisface esta condición.

Para distribuciones continuas de materia, el potencial gravitacional es:

\[\Phi = -G\int_V \frac{\rho(\mathbf{r\prime})}{r}dv^\prime \label{eqn:g_potential_v}\tag{7}\]

Para distribuciones superficiales de masa en cáscara delgada:

\[\Phi = -G\int_S \frac{\rho_s}{r}da^\prime. \label{eqn:g_potential_s}\tag{8}\]

Y para fuentes de masa lineales con densidad lineal $\rho_l$:

\[\Phi = -G\int_\Gamma \frac{\rho_l}{r}ds^\prime. \label{eqn:g_potential_l}\tag{9}\]

Significado físico

Consideremos el trabajo por unidad de masa $dW^\prime$ que realiza un objeto cuando se mueve una distancia $d\mathbf{r}$ en un campo gravitacional.

\[\begin{align*} dW^\prime &= -\mathbf{g}\cdot d\mathbf{r} = (\nabla \Phi)\cdot d\mathbf{r} \\ &= \sum_i \frac{\partial \Phi}{\partial x_i}dx_i = d\Phi \label{eqn:work}\tag{10} \end{align*}\]

En esta ecuación, $\Phi$ es función solo de las coordenadas de posición, expresada como $\Phi=\Phi(x_1, x_2, x_3) = \Phi(x_i)$. Por lo tanto, el trabajo por unidad de masa que realiza un objeto al moverse de un punto a otro en un campo gravitacional es igual a la diferencia de potencial entre esos dos puntos.

Si definimos el potencial gravitacional en el infinito como $0$, entonces $\Phi$ en cualquier punto puede interpretarse como el trabajo por unidad de masa necesario para mover el objeto desde el infinito hasta ese punto. La energía potencial del objeto es igual al producto de su masa y el potencial gravitacional $\Phi$, por lo que si $U$ es la energía potencial:

\[U = m\Phi. \label{eqn:potential_e}\tag{11}\]

Por lo tanto, la fuerza gravitacional que actúa sobre el objeto se obtiene aplicando el signo negativo al gradiente de su energía potencial.

\[\mathbf{F} = -\nabla U \label{eqn:force_and_potential}\tag{12}\]

Cuando un objeto está en un campo gravitacional creado por alguna masa, siempre existe cierta energía potencial. Esta energía potencial está estrictamente en el campo mismo, pero convencionalmente se expresa como la energía potencial del objeto.

Ejemplo: Potencial gravitacional dentro y fuera de una cáscara esférica (teorema de la cáscara)

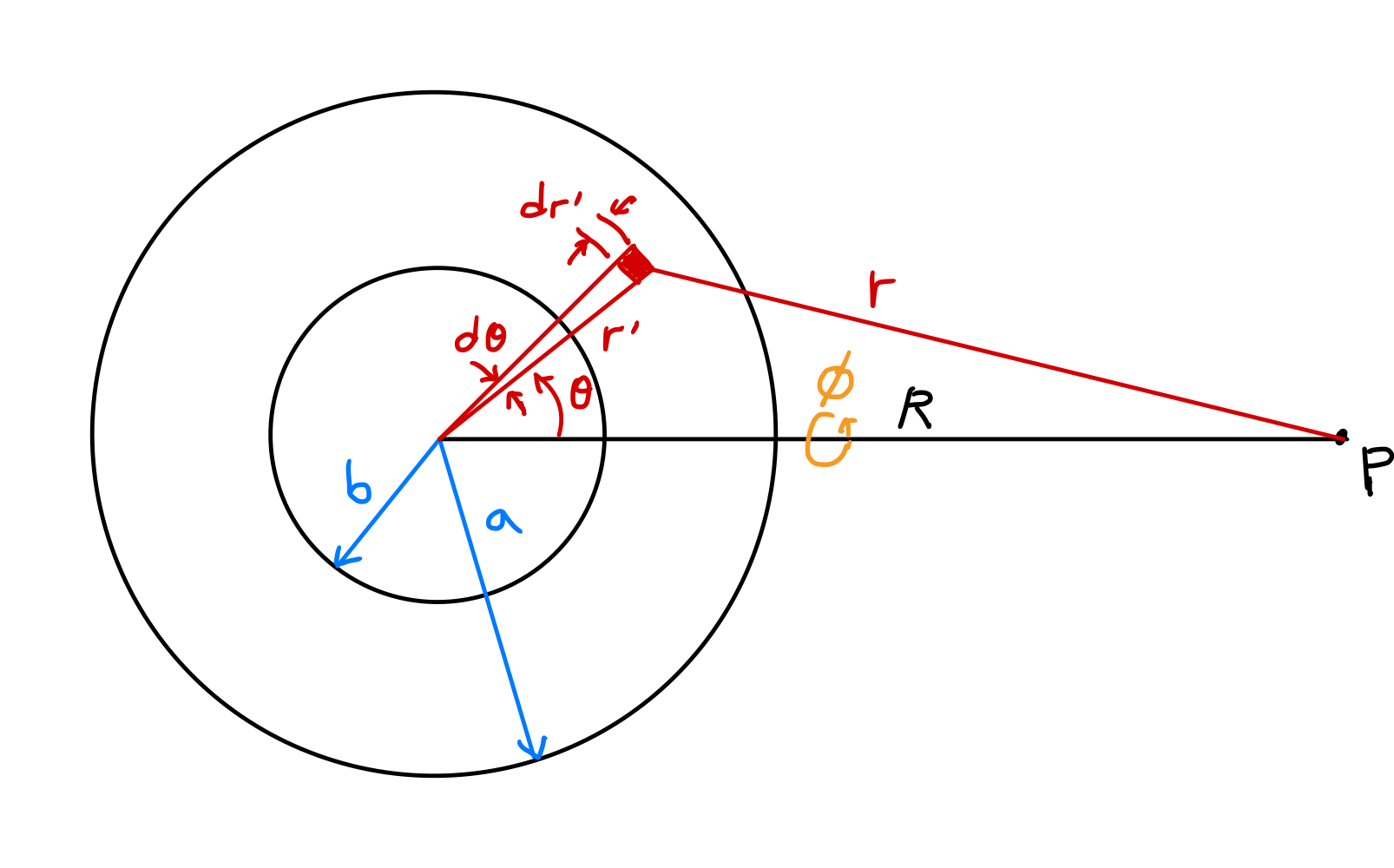
Configuración de coordenadas y expresión del potencial gravitacional como integral

Calculemos el potencial gravitacional dentro y fuera de una cáscara esférica uniforme con radio interno $b$ y radio externo $a$. Aunque la gravedad debida a la cáscara esférica también se puede obtener calculando directamente las componentes de fuerza que actúan sobre la masa unitaria en el campo, es más simple usar el método del potencial.

En la figura anterior, calculemos el potencial en el punto $P$ a distancia $R$ del centro. Asumiendo distribución uniforme de masa en la cáscara, $\rho(r^\prime)=\rho$, y por simetría respecto al ángulo azimutal $\phi$ alrededor de la línea que conecta el centro de la esfera con el punto $P$:

\[\begin{align*} \Phi &= -G\int_V \frac{\rho(r^\prime)}{r}dv^\prime \\ &= -\rho G \int_0^{2\pi} \int_0^\pi \int_b^a \frac{1}{r}(dr^\prime)(r^\prime d\theta)(r^\prime \sin\theta\, d\phi) \\ &= -\rho G \int_0^{2\pi} d\phi \int_b^a {r^\prime}^2 dr^\prime \int_0^\pi \frac{\sin\theta}{r}d\theta \\ &= -2\pi\rho G \int_b^a {r^\prime}^2 dr^\prime \int_0^\pi \frac{\sin\theta}{r}d\theta. \label{eqn:spherical_shell_1}\tag{13} \end{align*}\]

Según la ley de cosenos:

\[r^2 = {r^\prime}^2 + R^2 - 2r^\prime R \cos\theta \label{eqn:law_of_cosines}\tag{14}\]

Como $R$ es constante, diferenciando esta ecuación respecto a $r^\prime$:

\[2rdr = 2r^\prime R \sin\theta d\theta\] \[\frac{\sin\theta}{r}d\theta = \frac{dr}{r^\prime R} \tag{15}\]

Sustituyendo esto en la ecuación ($\ref{eqn:spherical_shell_1}$):

\[\Phi = -\frac{2\pi\rho G}{R} \int_b^a r^\prime dr^\prime \int_{r_\mathrm{min}}^{r_\mathrm{max}} dr. \label{eqn:spherical_shell_2}\tag{16}\]

Aquí, $r_\mathrm{max}$ y $r_\mathrm{min}$ se determinan según la posición del punto $P$.

Cuando $R>a$

\(\begin{align*} \Phi(R>a) &= -\frac{2\pi\rho G}{R} \int_b^a r^\prime dr^\prime \int_{R-r^\prime}^{R+r^\prime} dr \\ &= - \frac{4\pi\rho G}{R} \int_b^a {r^\prime}^2 dr^\prime \\ &= - \frac{4}{3}\frac{\pi\rho G}{R}(a^3 - b^3). \label{eqn:spherical_shell_outside_1}\tag{17} \end{align*}\)

La masa $M$ de la cáscara esférica es:

\[M = \frac{4}{3}\pi\rho(a^3 - b^3) \label{eqn:mass_of_shell}\tag{18}\]

Por lo tanto, el potencial es:

\[\boxed{\Phi(R>a) = -\frac{GM}{R}} \label{eqn:spherical_shell_outside_2}\tag{19}\]

Comparando la ecuación del potencial gravitacional debido a una masa puntual de masa $M$ ($\ref{eqn:g_potential}$) con el resultado que acabamos de obtener ($\ref{eqn:spherical_shell_outside_2}$), vemos que son idénticos. Esto significa que al calcular el potencial gravitacional en un punto externo debido a una distribución esféricamente simétrica de materia, se puede considerar que toda la masa está concentrada en el centro. La mayoría de los cuerpos celestes esféricos de cierto tamaño como la Tierra o la Luna corresponden a este caso, ya que pueden considerarse como infinitas cáscaras esféricas concéntricas de diferentes diámetros superpuestas como muñecas rusas. Esto proporciona la justificación para asumir cuerpos celestes como la Tierra o la Luna como masas puntuales sin tamaño mencionada al principio de este artículo.

Cuando $R<b$

\(\begin{align*} \Phi(R<b) &= -\frac{2\pi\rho G}{R} \int_b^a r^\prime dr^\prime \int_{r^\prime - R}^{r^\prime + R}dr \\ &= -4\pi\rho G \int_b^a r^\prime dr^\prime \\ &= -2\pi\rho G(a^2 - b^2). \label{eqn:spherical_shell_inside}\tag{20} \end{align*}\)

Dentro de una cáscara de masa esféricamente simétrica, el potencial gravitacional es constante independientemente de la posición, y la gravedad actuante es $0$.

Esto también es una de las principales evidencias de que la ‘teoría de la Tierra hueca’, una de las pseudociencias representativas, es absurda. Si la Tierra fuera una cáscara esférica con el interior vacío como afirma la teoría de la Tierra hueca, la gravedad terrestre no actuaría sobre ningún objeto dentro de esa cavidad. Considerando la masa y volumen de la Tierra, no puede haber una cavidad terrestre, y aunque la hubiera, las formas de vida allí no vivirían usando el interior de la cáscara esférica como suelo, sino que flotarían en estado de ingravidez como en una estación espacial.
Aunque pueden existir microorganismos en capas profundas del subsuelo a varios kilómetros bajo tierra, al menos no es posible de la forma que afirma la teoría de la Tierra hueca. Aunque me gusta mucho la novela de Julio Verne “Viaje al centro de la Tierra” y la película “Viaje al centro de la Tierra”, las obras de ficción deben disfrutarse como ficción, no creerse seriamente.

Cuando $b<R<a$

\(\begin{align*} \Phi(b<R<a) &= -\frac{4\pi\rho G}{3R}(R^3 - b^3) - 2\pi\rho G(a^2 - R^2) \\ &= -4\pi\rho G \left( \frac{a^2}{2} - \frac{b^3}{3R} - \frac{R^2}{6} \right) \label{eqn:within_spherical_shell}\tag{21} \end{align*}\)

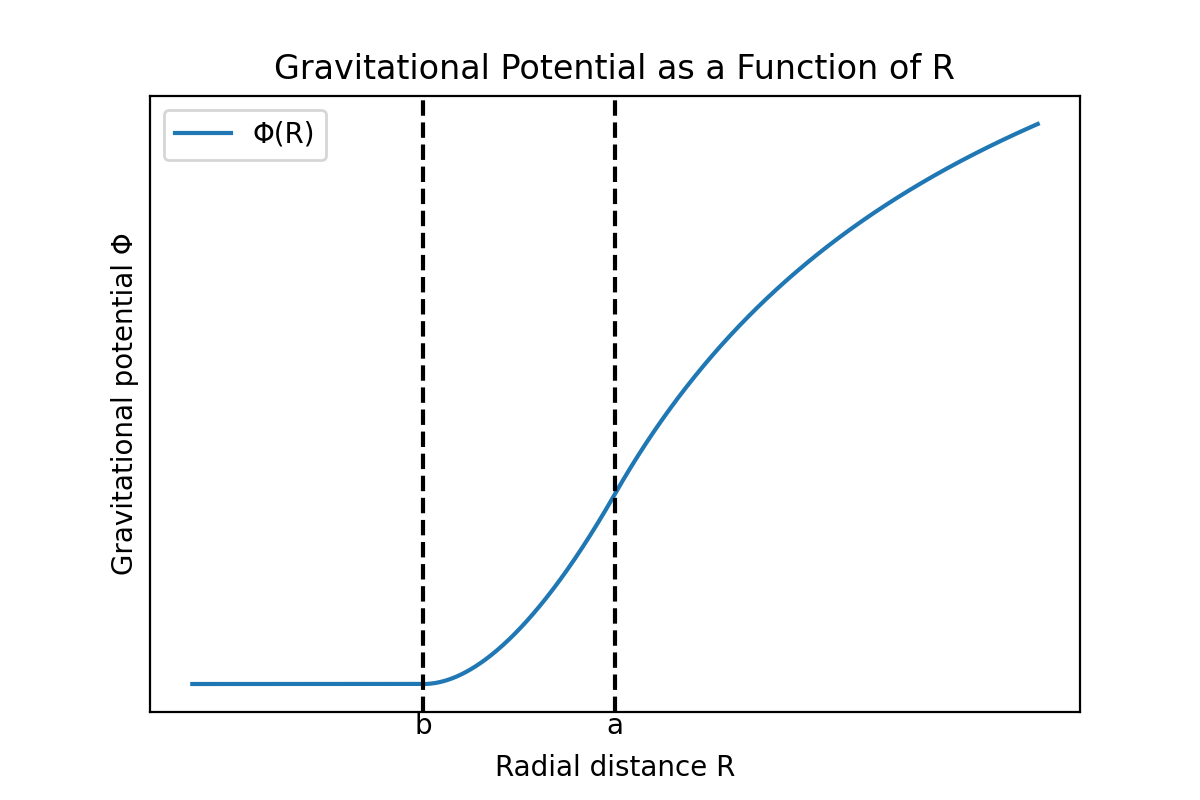
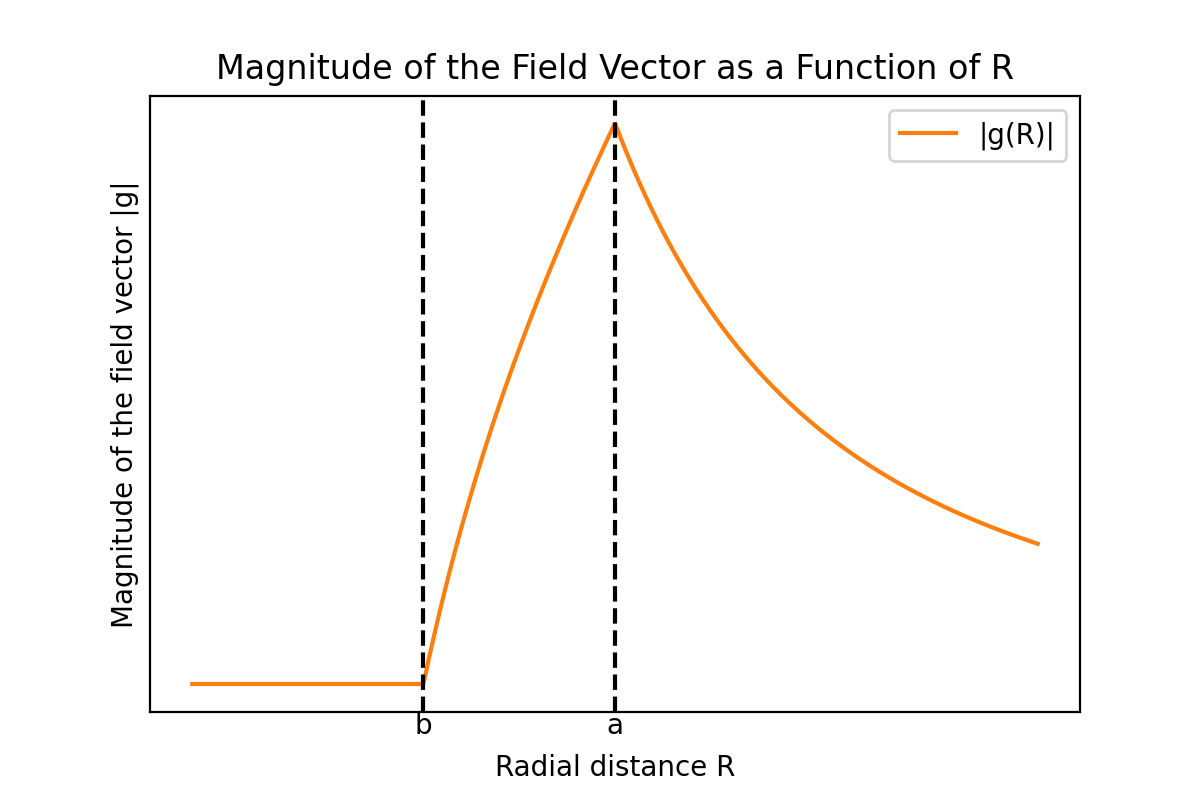
Resultados

Los potenciales gravitacionales $\Phi$ en las tres regiones calculadas anteriormente, y la magnitud correspondiente del vector de campo gravitacional $|\mathbf{g}|$ como función de la distancia $R$ se muestran gráficamente a continuación.

• Código de visualización en Python: repositorio yunseo-kim/physics-visualizations
• Licencia: Ver aquí

Se puede ver que tanto el potencial gravitacional como la magnitud del vector de campo gravitacional son continuos. Si el potencial gravitacional fuera discontinuo en algún punto, el gradiente del potencial en ese punto, es decir, la magnitud de la gravedad, se volvería infinita en ese punto, lo cual no es físicamente válido, por lo que la función potencial debe ser continua en todos los puntos. Sin embargo, la derivada del vector de campo gravitacional es discontinua en las superficies interna y externa de la cáscara.

Ejemplo: Curvas de rotación galáctica

Según observaciones astronómicas, en muchas galaxias espirales que rotan alrededor de su centro, como la Vía Láctea o la galaxia de Andrómeda, la mayoría de las masas observables se concentran cerca del centro. Sin embargo, las velocidades orbitales de las masas en estas galaxias espirales difieren significativamente de los valores predichos teóricamente a partir de la distribución de masa observable, como se puede confirmar en el siguiente gráfico, y son casi constantes más allá de cierta distancia.

Fuente de la imagen

• Autor: Usuario de Wikipedia PhilHibbs
• Licencia: Dominio Público

Curva de rotación de la galaxia espiral M33 (galaxia del Triángulo)

• Autor: Usuario de Wikimedia Mario De Leo
• Licencia: CC BY-SA 4.0

Predijamos la velocidad orbital según la distancia cuando la masa de la galaxia está concentrada en el centro, confirmemos que esta predicción no coincide con los resultados observacionales, y demostremos que la masa $M(R)$ distribuida dentro de la distancia $R$ desde el centro galáctico debe ser proporcional a $R$ para explicar los resultados observacionales.

Primero, si la masa galáctica $M$ está concentrada en el centro, la velocidad orbital a distancia $R$ es:

\[\frac{GMm}{R^2} = \frac{mv^2}{R}\] \[v = \sqrt{\frac{GM}{R}} \propto \frac{1}{\sqrt{R}}.\]

En este caso se predice una velocidad orbital que decrece como $1/\sqrt{R}$, como se muestra en las líneas punteadas de los dos gráficos anteriores, pero según los resultados observacionales, la velocidad orbital $v$ es casi constante independientemente de la distancia $R$, por lo que la predicción y los resultados observacionales no coinciden. Estos resultados observacionales solo pueden explicarse si $M(R)\propto R$.

Si escribimos $M(R) = kR$ usando la constante de proporcionalidad $k$:

\[v = \sqrt{\frac{GM(R)}{R}} = \sqrt{Gk}\ \text{(constante)}.\]

A partir de esto, los astrofísicos concluyen que debe haber ‘materia oscura’ no descubierta en muchas galaxias, y que esta materia oscura debe constituir más del 90% de la masa del universo. Sin embargo, la identidad de la materia oscura aún no se ha esclarecido claramente, y aunque no es la teoría principal, también existen intentos como la Dinámica Newtoniana Modificada (MOND) que trata de explicar los resultados observacionales sin asumir la existencia de materia oscura. Hoy en día, estos campos de investigación están en la vanguardia de la astrofísica.