La partícula libre

TL;DR

• Partícula libre: $V(x)=0$, sin condiciones de contorno (energía arbitraria)
• La solución separada $\Psi_k(x,t) = Ae^{i\left(kx-\frac{\hbar k^2}{2m}t \right)}$ diverge al infinito cuando se integra al cuadrado, por lo que no se puede normalizar, lo que sugiere:
  • Una partícula libre no puede existir en un estado estacionario
  • Una partícula libre no puede tener energía definida como un valor exacto (existe incertidumbre en la energía)
• Sin embargo, dado que la solución general de la ecuación de Schrödinger dependiente del tiempo es una combinación lineal de soluciones separadas, las soluciones separadas siguen teniendo importancia matemática. En este caso, como no hay condiciones restrictivas, la solución general toma la forma de una integral ($\int$) sobre la variable continua $k$ en lugar de una suma ($\sum$) sobre la variable discreta $n$.
• Solución general de la ecuación de Schrödinger:

\[\begin{gather*} \Psi(x,t) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \phi(k)e^{i(kx-\frac{\hbar k^2}{2m}t)}dk, \\ \text{donde }\phi(k) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\Psi(x,0)e^{-ikx}dx \end{gather*}\]

• Relación entre incertidumbre de posición e incertidumbre de momento:
  • Cuando la incertidumbre de posición disminuye, la incertidumbre de momento aumenta, y viceversa
  • Es decir, es imposible conocer simultáneamente con precisión la posición y el momento de una partícula libre en mecánica cuántica
• Velocidad de fase y velocidad de grupo de la función de onda $\Psi(x,t)$:
  • Velocidad de fase: $v_\text{phase} = \cfrac{\omega}{k} = \cfrac{\hbar k}{2m}$
  • Velocidad de grupo: $v_\text{group} = \cfrac{d\omega}{dk} = \cfrac{\hbar k}{m}$
• Significado físico de la velocidad de grupo y comparación con la mecánica clásica:
  • Físicamente, la velocidad de grupo representa la velocidad de movimiento de la partícula
  • Cuando $\phi(k)$ tiene una forma muy puntiaguda cerca de algún valor $k_0$ (cuando la incertidumbre del momento es suficientemente pequeña),

\[v_\text{group} = v_\text{classical} = \sqrt{\cfrac{2E}{m}}\]

Prerrequisitos

• Fórmula de Euler
• Transformada de Fourier & teorema de Plancherel
• Ecuación de Schrödinger y función de onda
• Ecuación de Schrödinger independiente del tiempo
• El pozo cuadrado infinito unidimensional

Configuración del modelo

Examinemos el caso más simple de una partícula libre ($V(x)=0$). Clásicamente, esto es simplemente movimiento a velocidad constante, pero en mecánica cuántica este problema es más interesante.
La ecuación de Schrödinger independiente del tiempo para una partícula libre es

\[-\frac{\hbar^2}{2m}\frac{d^2\psi}{dx^2}=E\psi \tag{1}\]

es decir

\[\frac{d^2\psi}{dx^2} = -k^2\psi \text{, donde }k\equiv \frac{\sqrt{2mE}}{\hbar} \label{eqn:t_independent_schrodinger_eqn}\tag{2}\]

Hasta aquí es igual que el interior de un pozo cuadrado infinito con potencial $0$. Sin embargo, esta vez escribamos la solución general en la siguiente forma exponencial.

\[\psi(x) = Ae^{ikx} + Be^{-ikx}. \tag{3}\]

$Ae^{ikx} + Be^{-ikx}$ y $C\cos{kx}+D\sin{kx}$ son formas equivalentes de escribir la misma función de $x$. Por la fórmula de Euler $e^{ix}=\cos{x}+i\sin{x}$,

\[\begin{align*} Ae^{ikx}+Be^{-ikx} &= A[\cos{kx}+i\sin{kx}] + B[\cos{(-kx)}+i\sin{(-kx)}] \\ &= A(\cos{kx}+i\sin{kx}) + B(\cos{kx}-i\sin{kx}) \\ &= (A+B)\cos{kx} + i(A-B)\sin{kx}. \end{align*}\]

Es decir, si establecemos $C=A+B$, $D=i(A-B)$, entonces

\[Ae^{ikx} + Be^{-ikx} = C\cos{kx}+D\sin{kx}. \blacksquare\]

Inversamente, si expresamos $A$ y $B$ en términos de $C$ y $D$, obtenemos $A=\cfrac{C-iD}{2}$, $B=\cfrac{C+iD}{2}$.

En mecánica cuántica, cuando $V=0$, las funciones exponenciales representan ondas en movimiento y son más convenientes al tratar partículas libres. Por otro lado, las funciones seno y coseno facilitan la representación de ondas estacionarias y aparecen naturalmente en el caso del pozo cuadrado infinito.

A diferencia del pozo cuadrado infinito, esta vez no hay condiciones de contorno que restrinjan $k$ y $E$. Es decir, una partícula libre puede tener cualquier energía positiva arbitraria.

Solución separada y velocidad de fase

Agregando la dependencia temporal $e^{-iEt/\hbar}$ a $\psi(x)$, obtenemos

\[\Psi(x,t) = Ae^{ik\left(x-\frac{\hbar k}{2m}t \right)} + Be^{-ik\left(x+\frac{\hbar k}{2m}t \right)} \label{eqn:Psi_seperated_solution}\tag{4}\]

Cualquier función arbitraria de $x$ y $t$ que dependa de esta forma especial $(x\pm vt)$ representa una onda que se mueve en la dirección $\mp x$ con velocidad $v$ sin cambiar de forma. Por lo tanto, el primer término de la ecuación ($\ref{eqn:Psi_seperated_solution}$) representa una onda que se mueve hacia la derecha, y el segundo término representa una onda que se mueve hacia la izquierda con la misma longitud de onda y velocidad de propagación pero diferente amplitud. Como solo difieren en el signo delante de $k$, podemos escribir

\[\Psi_k(x,t) = Ae^{i\left(kx-\frac{\hbar k^2}{2m}t \right)} \tag{5}\]

donde la dirección de propagación de la onda según el signo de $k$ es la siguiente.

\[k \equiv \pm\frac{\sqrt{2mE}}{\hbar},\quad \begin{cases} k>0 \Rightarrow & \text{movimiento hacia la derecha}, \\ k<0 \Rightarrow & \text{movimiento hacia la izquierda}. \end{cases} \tag{6}\]

El ‘estado estacionario’ de una partícula libre es claramente una onda propagante*, con longitud de onda $\lambda = 2\pi/|k|$ y por la fórmula de de Broglie

\[p = \frac{2\pi\hbar}{\lambda} = \hbar k \label{eqn:de_broglie_formula}\tag{7}\]

tiene momento.

*Es físicamente contradictorio que sea un ‘estado estacionario’ pero una onda propagante. La razón se verá pronto.

Además, la velocidad de esta onda es la siguiente.

\[v_{\text{phase}} = \left|\frac{\omega}{k}\right| = \frac{\hbar|k|}{2m} = \sqrt{\frac{E}{2m}}. \label{eqn:phase_velocity}\tag{8}\]

(Aquí $\omega$ es el coeficiente $\cfrac{\hbar k^2}{2m}$ delante de $t$.)

Sin embargo, esta función de onda no se puede normalizar porque diverge al infinito cuando se integra al cuadrado.

\[\int_{-\infty}^{\infty}\Psi_k^*\Psi_k dx = |A|^2\int_{-\infty}^{\infty}dx = \infty. \tag{9}\]

Es decir, en el caso de una partícula libre, la solución separada no es un estado físicamente posible. Una partícula libre no puede existir en un estado estacionario, ni puede tener algún valor específico de energía. De hecho, intuitivamente, es más extraño que se formen ondas estacionarias cuando no hay condiciones de contorno en ambos extremos.

Obtener la solución general $\Psi(x,t)$ de la ecuación de Schrödinger dependiente del tiempo

Sin embargo, esta solución separada sigue teniendo un significado importante porque, independientemente de la interpretación física, la solución general de la ecuación de Schrödinger dependiente del tiempo es una combinación lineal de soluciones separadas, lo que tiene un significado matemático. Sin embargo, en este caso, como no hay condiciones restrictivas, la solución general toma la forma de una integral ($\int$) sobre la variable continua $k$ en lugar de una suma ($\sum$) sobre la variable discreta $n$.

\[\Psi(x,t) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \phi(k)e^{i(kx-\frac{\hbar k^2}{2m}t)}dk. \label{eqn:Psi_general_solution}\tag{10}\]

Aquí $\cfrac{1}{\sqrt{2\pi}}\phi(k)dk$ juega el mismo papel que $c_n$ en la ecuación (21) del post ‘Ecuación de Schrödinger independiente del tiempo’.

Esta función de onda se puede normalizar para un $\phi(k)$ apropiado, pero necesariamente debe tener un rango de $k$ y por lo tanto un rango de energía y velocidad. Esto se llama paquete de ondas.

Las funciones seno se extienden infinitamente en el espacio, por lo que no se pueden normalizar. Sin embargo, cuando se superponen varias de estas ondas, se localizan por interferencia y se pueden normalizar.

Encontrar $\phi(k)$ usando el teorema de Plancherel

Ahora que conocemos la forma de $\Psi(x,t)$ (ecuación [$\ref{eqn:Psi_general_solution}$]), solo necesitamos determinar $\phi(k)$ que satisfaga la función de onda inicial

\[\Psi(x,0) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \phi(k)e^{ikx}dk \label{eqn:Psi_at_t_0}\tag{11}\]

Este es un problema típico del análisis de Fourier, y podemos obtener la respuesta con el teorema de Plancherel.

\[f(x) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} F(k)e^{ikx}dk \Longleftrightarrow F(k)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}f(x)e^{-ikx}dx. \label{eqn:plancherel_theorem}\tag{12}\]

$F(k)$ se llama transformada de Fourier de $f(x)$, y $f(x)$ se llama transformada inversa de Fourier de $F(k)$. Como se puede ver fácilmente en la ecuación ($\ref{eqn:plancherel_theorem}$), la única diferencia entre ambas es el signo del exponente. Por supuesto, existe la condición restrictiva de que solo se permiten funciones para las cuales existe la integral.

La condición necesaria y suficiente para que exista $f(x)$ es que $\int_{-\infty}^{\infty}|f(x)|^2dx$ sea finito. En este caso, $\int_{-\infty}^{\infty}|F(k)|^2dk$ también es finito, y

\[\int_{-\infty}^{\infty}|f(x)|^2 dx = \int_{-\infty}^{\infty}|F(k)|^2 dk\]

Algunas personas llaman a esta ecuación el teorema de Plancherel en lugar de la ecuación ($\ref{eqn:plancherel_theorem}$) (Wikipedia también lo describe así).

En este caso, la condición física de que $\Psi(x,0)$ debe estar normalizada garantiza que la integral existe. Por lo tanto, la solución mecánico-cuántica para una partícula libre es la ecuación ($\ref{eqn:Psi_general_solution}$), donde

\[\phi(k) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\Psi(x,0)e^{-ikx}dx \label{eqn:phi}\tag{13}\]

Sin embargo, en la práctica, rara vez se puede resolver analíticamente la integral de la ecuación ($\ref{eqn:Psi_general_solution}$). Generalmente se obtienen valores usando análisis numérico por computadora.

Cálculo de la velocidad de grupo del paquete de ondas e interpretación física

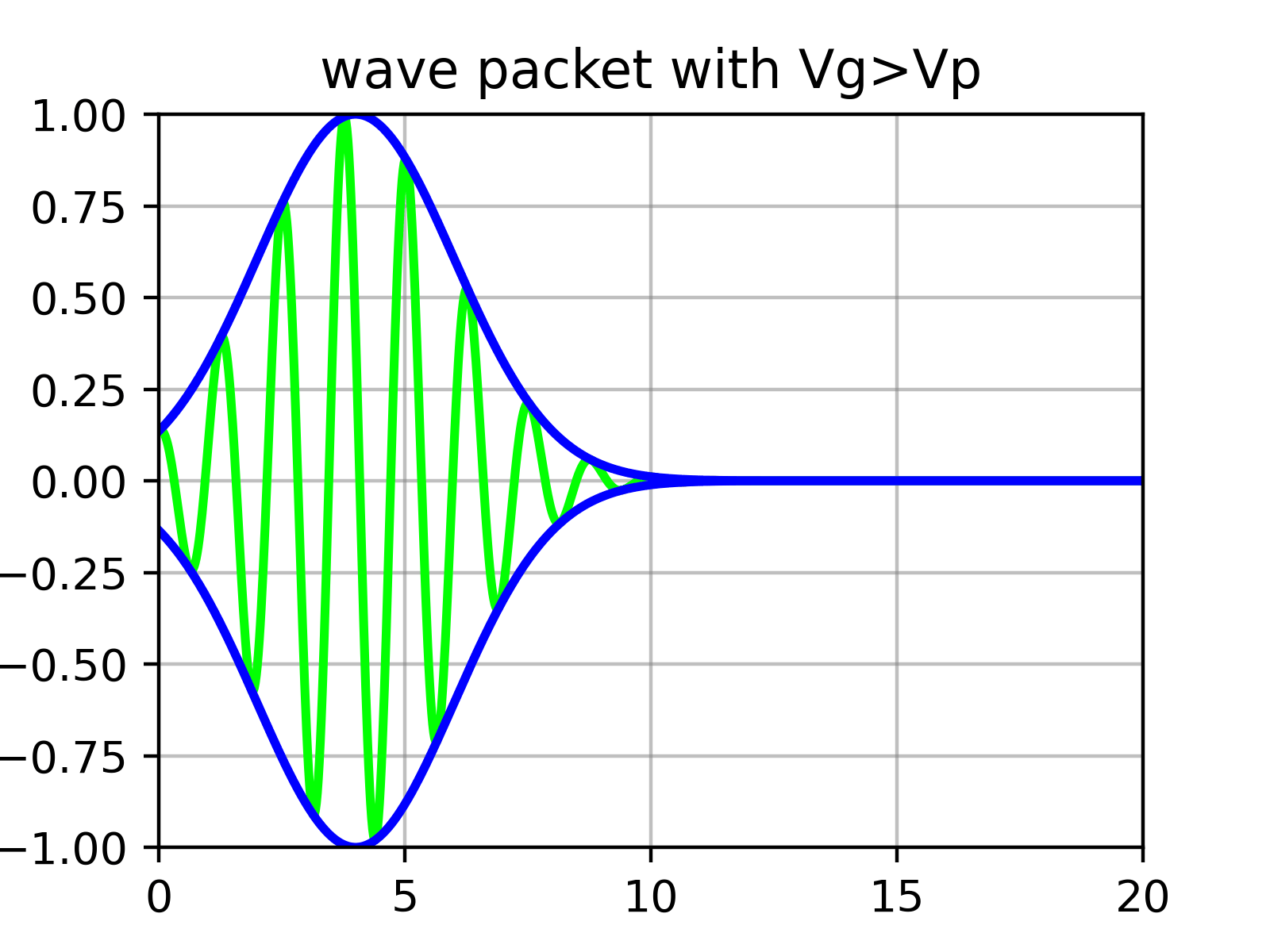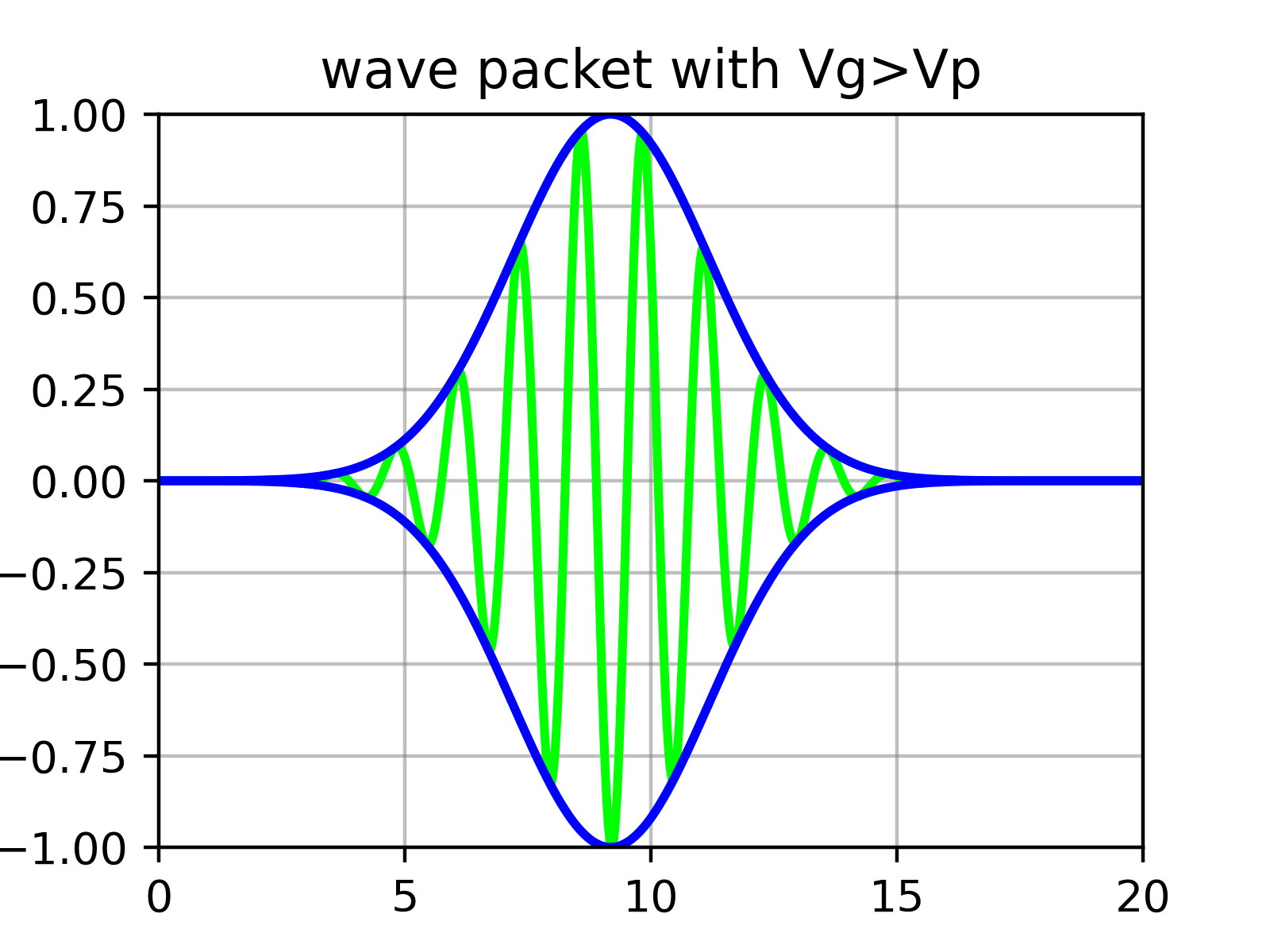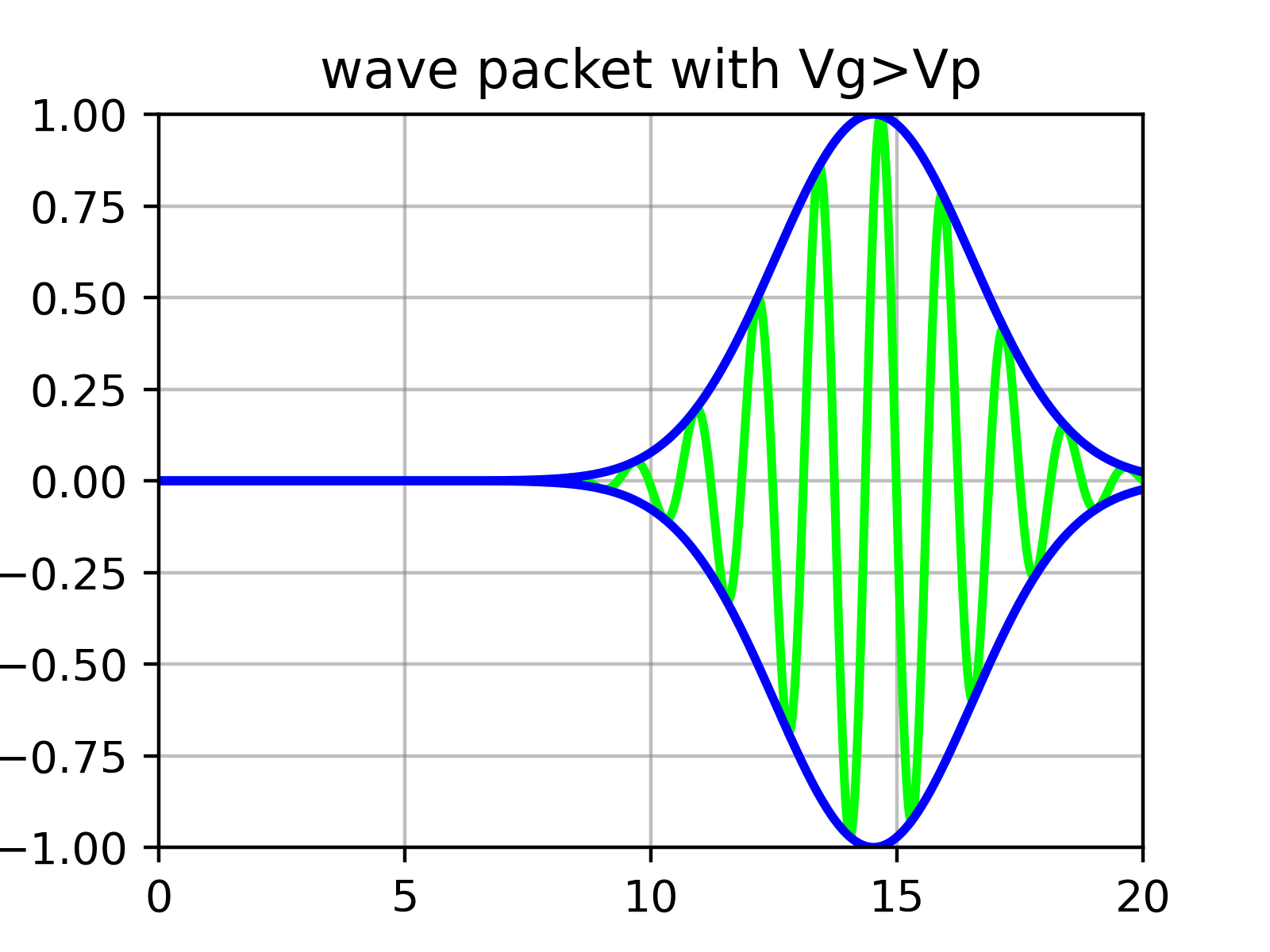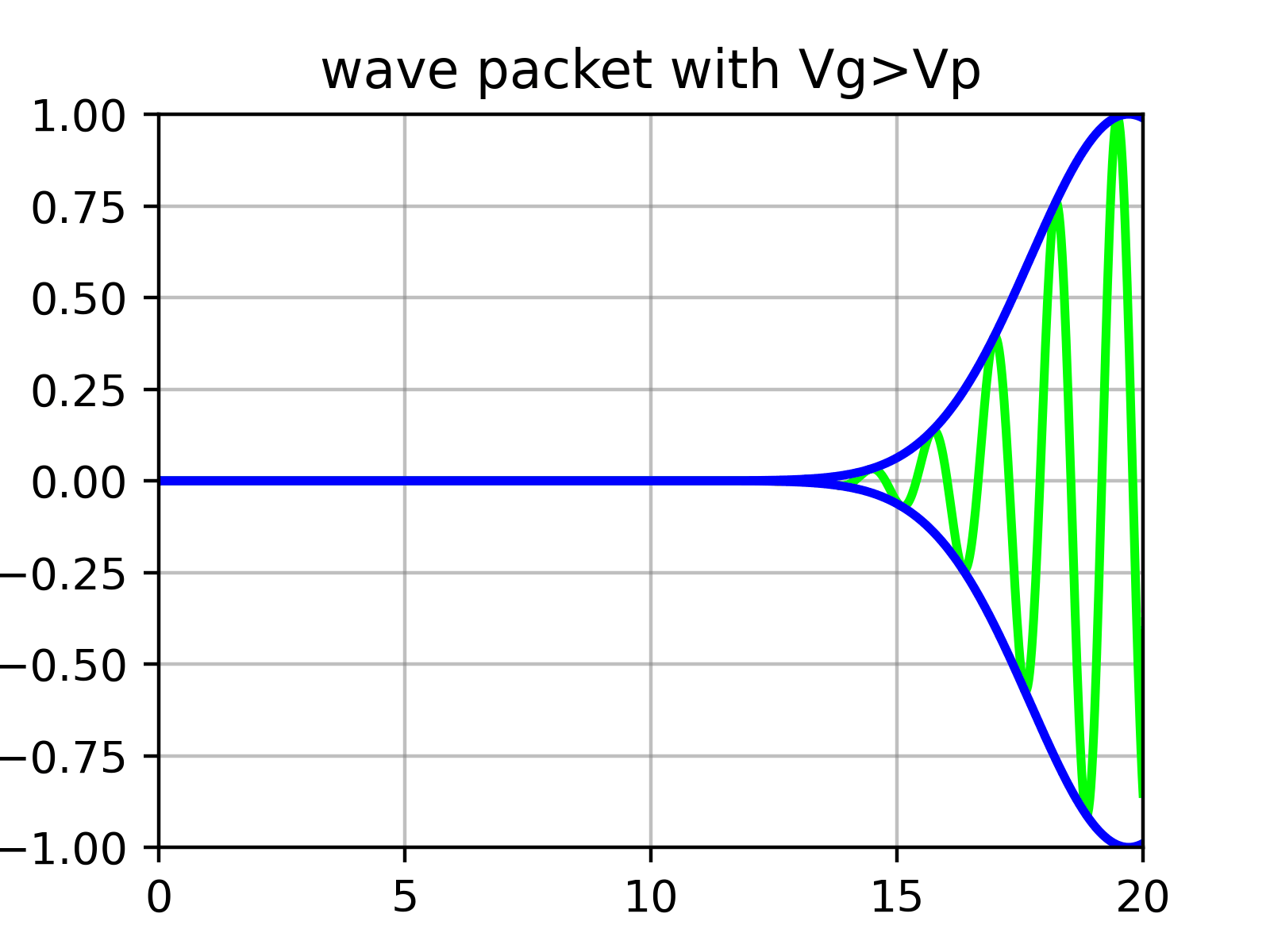
Esencialmente, un paquete de ondas es una superposición de numerosas funciones seno cuyas amplitudes están determinadas por $\phi$. Es decir, dentro de la ‘envolvente’ que forma el paquete de ondas hay ‘ondulaciones’.

Licencia de imagen y atribución de fuente original

• Código fuente de generación de imagen (gnuplot): yunseo-kim/physics-visualizations
• Licencia: Mozilla Public License 2.0
• Autor original: Ph.D. Youjun Hu
• Aviso de licencia original: MIT License

Físicamente, lo que corresponde a la velocidad de la partícula no es la velocidad de las ondulaciones individuales (velocidad de fase) calculada anteriormente en la ecuación ($\ref{eqn:phase_velocity}$), sino la velocidad de la envolvente exterior (velocidad de grupo).

Relación entre incertidumbre de posición e incertidumbre de momento

Examinemos la relación entre la incertidumbre de posición y la incertidumbre de momento considerando por separado las partes del integrando $\int\phi(k)e^{ikx}dk$ de la ecuación ($\ref{eqn:Psi_at_t_0}$) y $\int\Psi(x,0)e^{-ikx}dx$ de la ecuación ($\ref{eqn:phi}$).

Cuando la incertidumbre de posición es pequeña

Cuando $\Psi$ en el espacio de posición se distribuye en una región muy estrecha $[x_0-\delta, x_0+\delta]$ alrededor de algún valor $x_0$ y es cercana a 0 en otras regiones (cuando la incertidumbre de posición es pequeña), $e^{-ikx} \approx e^{-ikx_0}$ es casi constante respecto a $x$, por lo que

\[\begin{align*} \int_{-\infty}^{\infty} \Psi(x,0)e^{-ikx}dx &\approx \int_{x_0-\delta}^{x_0+\delta} \Psi(x,0)e^{-ikx_0}dx \\ &= e^{-ikx_0}\int_{x_0-\delta}^{x_0+\delta} \Psi(x,0)dx \\ &= e^{-ipx_0/\hbar}\int_{x_0-\delta}^{x_0+\delta} \Psi(x,0)dx \quad (\because \text{eqn. }\ref{eqn:de_broglie_formula}) \end{align*}\tag{14}\]

Como el término de la integral definida es constante respecto a $p$, $\phi$ toma la forma de una onda seno respecto a $p$ en el espacio de momento debido al término $e^{-ipx_0/\hbar}$ del frente, es decir, se distribuye en un amplio rango de momento (la incertidumbre de momento es grande).

Cuando la incertidumbre de momento es pequeña

De manera similar, cuando $\phi$ en el espacio de momento se distribuye en una región muy estrecha $[p_0-\delta, p_0+\delta]$ alrededor de algún valor $p_0$ y es cercana a 0 en otras regiones (cuando la incertidumbre de momento es pequeña), por la ecuación ($\ref{eqn:de_broglie_formula}$), $e^{ikx}=e^{ipx/\hbar} \approx e^{ip_0x/\hbar}$ es casi constante respecto a $p$ y $dk=\frac{1}{\hbar}dp$, por lo que

\[\begin{align*} \int_{-\infty}^{\infty} \phi(k)e^{ikx}dk &= \frac{1}{\hbar}\int_{p_0-\delta}^{p_0+\delta} \phi(p)e^{ip_0x/\hbar}dp \\ &= \frac{1}{\hbar}e^{ip_0x/\hbar}\int_{p_0-\delta}^{p_0+\delta} \phi(p)dp \end{align*}\tag{15}\]

Debido al término $e^{ip_0x/\hbar}$ del frente, $\Psi$ toma la forma de una onda seno respecto a $x$ en el espacio de posición, es decir, se distribuye en un amplio rango de posición (la incertidumbre de posición es grande).

Conclusión

Cuando la incertidumbre de posición disminuye, la incertidumbre de momento aumenta, y viceversa, cuando la incertidumbre de momento disminuye, la incertidumbre de posición aumenta. Por lo tanto, es imposible conocer simultáneamente con precisión la posición y el momento de una partícula libre en mecánica cuántica.

Fuente de imagen

• Autor: Usuario de Wikipedia en inglés Maschen
• Licencia: dominio público

De hecho, por el principio de incertidumbre, esto se aplica no solo a partículas libres sino a todos los casos. El principio de incertidumbre se tratará en un post separado en el futuro.

Velocidad de grupo del paquete de ondas

Reescribiendo la solución general de la ecuación ($\ref{eqn:Psi_general_solution}$) con $\omega \equiv \cfrac{\hbar k^2}{2m}$ como en la ecuación ($\ref{eqn:phase_velocity}$),

\[\Psi(x,t) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \phi(k)e^{i(kx-\omega t)}dk \tag{16}\]

La ecuación que expresa $\omega$ como función de $k$, como $\omega = \cfrac{\hbar k^2}{2m}$, se llama relación de dispersión. El contenido que se describe a continuación se aplica generalmente a todos los paquetes de ondas independientemente de la relación de dispersión.

Ahora supongamos que $\phi(k)$ tiene una forma muy puntiaguda cerca de algún valor apropiado $k_0$. (Aunque puede estar ampliamente distribuido respecto a $k$, tal paquete de ondas se deforma muy rápidamente y cambia a otra forma. Esto se debe a que los componentes para diferentes $k$ se mueven a velocidades diferentes, perdiendo el significado de un ‘grupo’ completo con una velocidad bien definida. Es decir, la incertidumbre del momento aumenta.)
Como la función integrada es despreciable excepto cerca de $k_0$, podemos expandir en serie de Taylor la función $\omega(k)$ cerca de este punto, y escribiendo solo hasta el término de primer orden,

\[\omega(k) \approx \omega_0 + \omega_0^\prime(k-k_0)\]

Ahora, sustituyendo $s=k-k_0$ e integrando centrado en $k_0$,

\[\begin{align*} \Psi(x,t) &= \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\phi(k_0+s)e^{i[(k_0+s)x-(\omega_0+\omega_0^\prime s)t]}ds \\ &= \frac{1}{\sqrt{2\pi}}e^{i(k_0x-\omega_0t)}\int_{-\infty}^{\infty}\phi(k_0+s)e^{is(x-\omega_0^\prime t)}ds. \end{align*}\tag{17}\]

El término del frente $e^{i(k_0x-\omega_0t)}$ representa una onda seno (‘ondulación’) que se mueve con velocidad $\omega_0/k_0$, y el término integral que determina la amplitud de esta onda seno (‘envolvente’) se mueve con velocidad $\omega_0^\prime$ debido a la parte $e^{is(x-\omega_0^\prime t)}$. Por lo tanto, la velocidad de fase en $k=k_0$ es

\[v_\text{phase} = \frac{\omega_0}{k_0} = \frac{\omega}{k} = \frac{\hbar k}{2m} \tag{18}\]

confirmando nuevamente que es igual al valor de la ecuación ($\ref{eqn:phase_velocity}$), y la velocidad de grupo es

\[v_\text{group} = \omega_0^\prime = \frac{d\omega}{dk} = \frac{\hbar k}{m} \label{eqn:group_velocity}\tag{19}\]

que es el doble de la velocidad de fase.

Comparación con la mecánica clásica

Como sabemos que la mecánica clásica se cumple a escala macroscópica, los resultados obtenidos a través de la mecánica cuántica deben poder aproximarse a los resultados calculados en mecánica clásica cuando la incertidumbre cuántica es suficientemente pequeña. En el caso de la partícula libre que estamos tratando, cuando $\phi(k)$ tiene una forma muy puntiaguda cerca del valor apropiado $k_0$ como asumimos anteriormente (es decir, cuando la incertidumbre del momento es suficientemente pequeña), la velocidad de grupo $v_\text{group}$ que corresponde a la velocidad de la partícula en mecánica cuántica debe ser igual a la velocidad de la partícula $v_\text{classical}$ obtenida en mecánica clásica para los mismos valores de $k$ y la energía correspondiente $E$.

Sustituyendo $k\equiv \cfrac{\sqrt{2mE}}{\hbar}$ de la ecuación ($\ref{eqn:t_independent_schrodinger_eqn}$) en la velocidad de grupo recién obtenida (ecuación [$\ref{eqn:group_velocity}$]),

\[v_\text{quantum} = \sqrt{\frac{2E}{m}} \tag{20}\]

y en mecánica clásica, la velocidad de una partícula libre con energía cinética $E$ es igualmente

\[v_\text{classical} = \sqrt{\frac{2E}{m}} \tag{21}\]

Por lo tanto, como $v_\text{quantum}=v_\text{classical}$, podemos confirmar que el resultado obtenido aplicando mecánica cuántica es una solución físicamente válida.