Champ gravitationnel et potentiel gravitationnel

TL;DR

• Loi de la gravitation universelle de Newton : $\mathbf{F} = -G\cfrac{mM}{r^2}\mathbf{e}_r$
• Pour les objets ayant une distribution de masse continue et une taille : $\mathbf{F} = -Gm\int_V \cfrac{dM}{r^2}\mathbf{e}_r = -Gm\int_V \cfrac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2} dv^{\prime}$
  • $\rho(\mathbf{r^{\prime}})$ : densité de masse au point situé au vecteur position $\mathbf{r^{\prime}}$ depuis une origine arbitraire
  • $dv^{\prime}$ : élément de volume au point situé au vecteur position $\mathbf{r^{\prime}}$ depuis une origine arbitraire
• Vecteur champ gravitationnel :
  • Vecteur représentant la force par unité de masse qu’une particule reçoit dans un champ créé par un objet de masse $M$
  • $\mathbf{g} = \cfrac{\mathbf{F}}{m} = - G \cfrac{M}{r^2}\mathbf{e}_r = - G \int_V \cfrac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2}dv^\prime$
  • Dimension de force par unité de masse ou d’accélération
• Potentiel gravitationnel :
  • $\mathbf{g} \equiv -\nabla \Phi$
  • Dimension de (force par unité de masse) × (distance) ou d’énergie par unité de masse
  • $\Phi = -G\cfrac{M}{r}$
  • Seule la différence relative du potentiel gravitationnel a un sens, pas une valeur spécifique
  • On fixe généralement la condition $\Phi \to 0$ quand $r \to \infty$ pour éliminer l’ambiguïté
  • $U = m\Phi, \quad \mathbf{F} = -\nabla U$
• Potentiel gravitationnel à l’intérieur et à l’extérieur d’une coquille sphérique (théorème de la coquille)
  • Quand $R>a$ :
    • $\Phi(R>a) = -\cfrac{GM}{R}$
    • Pour calculer le potentiel gravitationnel en un point extérieur dû à une distribution de matière à symétrie sphérique, on peut considérer l’objet comme une masse ponctuelle
  • Quand $R<b$ :
    • $\Phi(R<b) = -2\pi\rho G(a^2 - b^2)$
    • À l’intérieur d’une coquille de masse à symétrie sphérique, le potentiel gravitationnel est constant indépendamment de la position, et la gravité exercée est nulle
  • Quand $b<R<a$ : $\Phi(b<R<a) = -4\pi\rho G \left( \cfrac{a^2}{2} - \cfrac{b^3}{3R} - \cfrac{R^2}{6} \right)$

Champ gravitationnel

Loi de la gravitation universelle de Newton

Newton avait déjà systématisé et vérifié numériquement la loi de la gravitation universelle avant 11666 HE. Cependant, il fallut encore 20 ans avant qu’il publie ses résultats dans son ouvrage Principia en 11687 HE, car il ne pouvait pas justifier la méthode de calcul qui supposait que la Terre et la Lune étaient des masses ponctuelles sans taille. Heureusement, en utilisant le calcul différentiel que Newton inventa par la suite, nous pouvons démontrer beaucoup plus facilement ce problème qui n’était pas simple pour Newton dans les années 11600.

Selon la loi de la gravitation universelle de Newton, chaque particule de masse attire toutes les autres particules de l’univers avec une force proportionnelle au produit des deux masses et inversement proportionnelle au carré de la distance qui les sépare. Mathématiquement, cela s’exprime comme suit :

\[\mathbf{F} = -G\frac{mM}{r^2}\mathbf{e}_r \label{eqn:law_of_gravitation}\tag{1}\]

Source de l’image

• Auteur : utilisateur Wikimedia Dennis Nilsson
• Licence : CC BY 3.0

Le vecteur unitaire $\mathbf{e}_r$ pointe de $M$ vers $m$, et le signe négatif indique que la force est attractive. Autrement dit, $m$ est attiré vers $M$.

Expérience de Cavendish

La vérification expérimentale de cette loi et la détermination de la valeur de $G$ furent réalisées en 11798 HE par le physicien britannique Henry Cavendish. L’expérience de Cavendish utilise une balance de torsion constituée de deux petites sphères fixées aux extrémités d’une tige légère. Ces deux sphères sont chacune attirées vers deux autres grosses sphères situées à proximité. La valeur officielle de $G$ déterminée à ce jour est $6.673 \pm 0.010 \times 10^{-11} \mathrm{N\cdot m^2/kg^2}$.

Bien que $G$ soit l’une des constantes fondamentales connues depuis le plus longtemps, elle n’est connue qu’avec une précision plus faible que la plupart des autres constantes fondamentales comme $e$, $c$, $\hbar$. Aujourd’hui encore, de nombreuses recherches sont menées pour déterminer la valeur de $G$ avec une plus grande précision.

Cas d’objets ayant une taille

La loi de l’équation ($\ref{eqn:law_of_gravitation}$) ne s’applique rigoureusement qu’aux particules ponctuelles. Si l’un ou les deux objets ont une taille, il faut ajouter l’hypothèse supplémentaire que le champ gravitationnel est un champ linéaire pour calculer la force. Autrement dit, on suppose que la gravité totale qu’une particule de masse $m$ reçoit de plusieurs autres particules peut être obtenue en additionnant vectoriellement chaque force. Pour les objets à distribution de matière continue, on remplace la somme par une intégrale comme suit :

\[\mathbf{F} = -Gm\int_V \frac{dM}{r^2}\mathbf{e}_r = -Gm\int_V \frac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2} dv^{\prime} \label{eqn:integral_form}\tag{2}\]

• $\rho(\mathbf{r^{\prime}})$ : densité de masse au point situé au vecteur position $\mathbf{r^{\prime}}$ depuis une origine arbitraire
• $dv^{\prime}$ : élément de volume au point situé au vecteur position $\mathbf{r^{\prime}}$ depuis une origine arbitraire

Si les objets de masse $M$ et de masse $m$ ont tous deux une taille et qu’on veut calculer la gravité totale, une seconde intégrale de volume sur $m$ est également nécessaire.

Vecteur champ gravitationnel

Le vecteur champ gravitationnel $\mathbf{g}$ est défini comme le vecteur représentant la force par unité de masse qu’une particule reçoit dans un champ créé par un objet de masse $M$ :

\[\mathbf{g} = \frac{\mathbf{F}}{m} = - G \frac{M}{r^2}\mathbf{e}_r \label{eqn:g_vector}\tag{3}\]

ou

\[\boxed{\mathbf{g} = - G \int_V \frac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2}dv^\prime} \tag{4}\]

Ici, la direction de $\mathbf{e}_r$ varie selon $\mathbf{r^\prime}$.

Cette quantité $\mathbf{g}$ a la dimension de force par unité de masse ou d’accélération. La magnitude du vecteur champ gravitationnel $\mathbf{g}$ près de la surface terrestre est égale à ce que nous appelons la constante d’accélération gravitationnelle, avec $|\mathbf{g}| \approx 9.80\mathrm{m/s^2}$.

Potentiel gravitationnel

Définition

Le vecteur champ gravitationnel $\mathbf{g}$ varie en $1/r^2$, et satisfait donc la condition ($\nabla \times \mathbf{g} \equiv 0$) pour être exprimé comme le gradient d’une fonction scalaire (potentiel). On peut donc écrire :

\[\mathbf{g} \equiv -\nabla \Phi \label{eqn:gradient_phi}\tag{5}\]

où $\Phi$ est appelé potentiel gravitationnel, et a la dimension de (force par unité de masse) × (distance) ou d’énergie par unité de masse.

Puisque $\mathbf{g}$ ne dépend que du rayon, $\Phi$ varie également selon $r$. À partir des équations ($\ref{eqn:g_vector}$) et ($\ref{eqn:gradient_phi}$) :

\[\nabla\Phi = \frac{d\Phi}{dr}\mathbf{e}_r = G\frac{M}{r^2}\mathbf{e}_r\]

En intégrant, on obtient :

\[\boxed{\Phi = -G\frac{M}{r}} \label{eqn:g_potential}\tag{6}\]

Puisque seule la différence relative du potentiel gravitationnel a un sens et non la magnitude d’une valeur absolue, on peut omettre la constante d’intégration. On fixe généralement la condition $\Phi \to 0$ quand $r \to \infty$ pour éliminer l’ambiguïté, et l’équation ($\ref{eqn:g_potential}$) satisfait également cette condition.

Le potentiel gravitationnel pour une distribution continue de matière est :

\[\Phi = -G\int_V \frac{\rho(\mathbf{r\prime})}{r}dv^\prime \label{eqn:g_potential_v}\tag{7}\]

Pour une distribution surfacique de masse sur une coquille mince :

\[\Phi = -G\int_S \frac{\rho_s}{r}da^\prime. \label{eqn:g_potential_s}\tag{8}\]

Et pour une source de masse linéaire de densité linéaire $\rho_l$ :

\[\Phi = -G\int_\Gamma \frac{\rho_l}{r}ds^\prime. \label{eqn:g_potential_l}\tag{9}\]

Signification physique

Considérons le travail par unité de masse $dW^\prime$ qu’un objet effectue lorsqu’il se déplace de $d\mathbf{r}$ dans un champ gravitationnel.

\[\begin{align*} dW^\prime &= -\mathbf{g}\cdot d\mathbf{r} = (\nabla \Phi)\cdot d\mathbf{r} \\ &= \sum_i \frac{\partial \Phi}{\partial x_i}dx_i = d\Phi \label{eqn:work}\tag{10} \end{align*}\]

Dans cette équation, $\Phi$ est une fonction des seules coordonnées de position, exprimée comme $\Phi=\Phi(x_1, x_2, x_3) = \Phi(x_i)$. On peut donc voir que le travail par unité de masse qu’un objet effectue lorsqu’il se déplace d’un point à un autre dans un champ gravitationnel est égal à la différence de potentiel entre ces deux points.

Si on définit le potentiel gravitationnel à l’infini comme $0$, alors $\Phi$ en un point quelconque peut être interprété comme le travail par unité de masse nécessaire pour déplacer l’objet de l’infini jusqu’à ce point. L’énergie potentielle d’un objet est égale au produit de sa masse et du potentiel gravitationnel $\Phi$, donc si $U$ est l’énergie potentielle :

\[U = m\Phi. \label{eqn:potential_e}\tag{11}\]

Par conséquent, la gravité qu’un objet subit s’obtient en appliquant un signe négatif au gradient de son énergie potentielle.

\[\mathbf{F} = -\nabla U \label{eqn:force_and_potential}\tag{12}\]

Lorsqu’un objet est placé dans un champ gravitationnel créé par une masse, il y a toujours une énergie potentielle. Cette énergie potentielle appartient strictement au champ lui-même, mais par convention, on l’exprime comme l’énergie potentielle de l’objet.

Exemple : Potentiel gravitationnel à l’intérieur et à l’extérieur d’une coquille sphérique (théorème de la coquille)

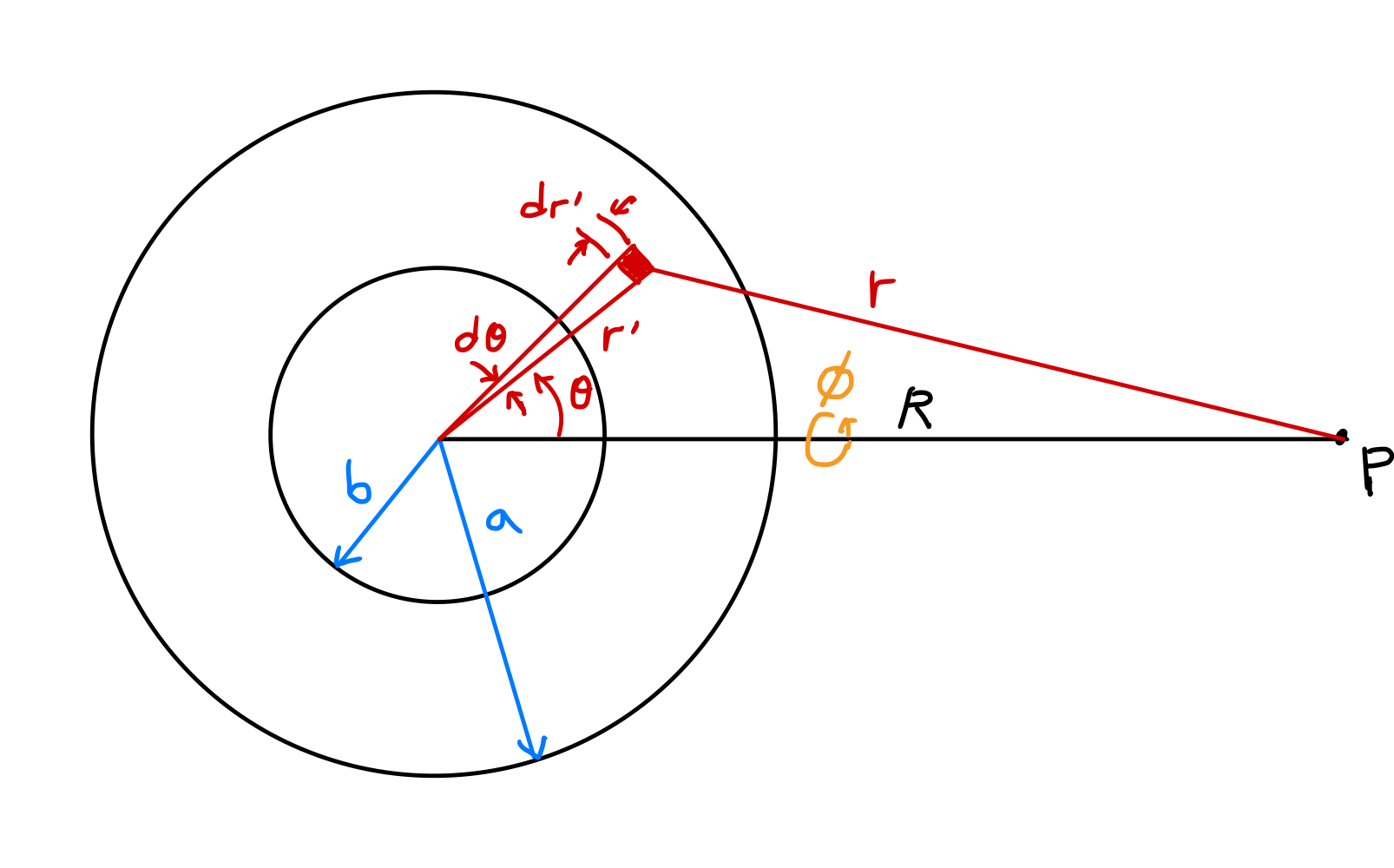
Configuration des coordonnées et expression du potentiel gravitationnel par intégrale

Calculons le potentiel gravitationnel à l’intérieur et à l’extérieur d’une coquille sphérique uniforme de rayon intérieur $b$ et de rayon extérieur $a$. Bien qu’on puisse obtenir la gravité due à la coquille sphérique en calculant directement les composantes de force agissant sur une masse unitaire dans le champ, la méthode du potentiel est plus simple.

Calculons le potentiel au point $P$ situé à une distance $R$ du centre dans la figure ci-dessus. En supposant une distribution de masse uniforme de la coquille, $\rho(r^\prime)=\rho$, et par symétrie par rapport à l’angle azimutal $\phi$ autour de la ligne reliant le centre de la sphère au point $P$ :

\[\begin{align*} \Phi &= -G\int_V \frac{\rho(r^\prime)}{r}dv^\prime \\ &= -\rho G \int_0^{2\pi} \int_0^\pi \int_b^a \frac{1}{r}(dr^\prime)(r^\prime d\theta)(r^\prime \sin\theta\, d\phi) \\ &= -\rho G \int_0^{2\pi} d\phi \int_b^a {r^\prime}^2 dr^\prime \int_0^\pi \frac{\sin\theta}{r}d\theta \\ &= -2\pi\rho G \int_b^a {r^\prime}^2 dr^\prime \int_0^\pi \frac{\sin\theta}{r}d\theta. \label{eqn:spherical_shell_1}\tag{13} \end{align*}\]

Selon la loi des cosinus :

\[r^2 = {r^\prime}^2 + R^2 - 2r^\prime R \cos\theta \label{eqn:law_of_cosines}\tag{14}\]

et puisque $R$ est constant, en dérivant cette équation par rapport à $r^\prime$ :

\[2rdr = 2r^\prime R \sin\theta d\theta\] \[\frac{\sin\theta}{r}d\theta = \frac{dr}{r^\prime R} \tag{15}\]

En substituant ceci dans l’équation ($\ref{eqn:spherical_shell_1}$) :

\[\Phi = -\frac{2\pi\rho G}{R} \int_b^a r^\prime dr^\prime \int_{r_\mathrm{min}}^{r_\mathrm{max}} dr. \label{eqn:spherical_shell_2}\tag{16}\]

où $r_\mathrm{max}$ et $r_\mathrm{min}$ sont déterminés par la position du point $P$.

Quand $R>a$

\(\begin{align*} \Phi(R>a) &= -\frac{2\pi\rho G}{R} \int_b^a r^\prime dr^\prime \int_{R-r^\prime}^{R+r^\prime} dr \\ &= - \frac{4\pi\rho G}{R} \int_b^a {r^\prime}^2 dr^\prime \\ &= - \frac{4}{3}\frac{\pi\rho G}{R}(a^3 - b^3). \label{eqn:spherical_shell_outside_1}\tag{17} \end{align*}\)

La masse $M$ de la coquille sphérique est :

\[M = \frac{4}{3}\pi\rho(a^3 - b^3) \label{eqn:mass_of_shell}\tag{18}\]

donc le potentiel est :

\[\boxed{\Phi(R>a) = -\frac{GM}{R}} \label{eqn:spherical_shell_outside_2}\tag{19}\]

En comparant le potentiel gravitationnel dû à une masse ponctuelle $M$ de l’équation ($\ref{eqn:g_potential}$) avec le résultat que nous venons d’obtenir ($\ref{eqn:spherical_shell_outside_2}$), on voit qu’ils sont identiques. Cela signifie que pour calculer le potentiel gravitationnel en un point extérieur dû à une distribution de matière à symétrie sphérique, on peut considérer que toute la masse est concentrée au centre. Ceci s’applique à la plupart des corps célestes sphériques d’une certaine taille comme la Terre ou la Lune, qui peuvent être considérés comme une superposition d’innombrables coquilles sphériques concentriques de différents diamètres, comme des poupées russes. Ceci constitue la justification pour supposer que des corps célestes comme la Terre ou la Lune sont des masses ponctuelles sans taille lors des calculs.

Quand $R<b$

\(\begin{align*} \Phi(R<b) &= -\frac{2\pi\rho G}{R} \int_b^a r^\prime dr^\prime \int_{r^\prime - R}^{r^\prime + R}dr \\ &= -4\pi\rho G \int_b^a r^\prime dr^\prime \\ &= -2\pi\rho G(a^2 - b^2). \label{eqn:spherical_shell_inside}\tag{20} \end{align*}\)

À l’intérieur d’une coquille de masse à symétrie sphérique, le potentiel gravitationnel est constant indépendamment de la position, et la gravité exercée est nulle.

Ceci constitue également une preuve majeure que la “théorie de la Terre creuse”, l’une des pseudosciences représentatives, est absurde. Si la Terre était une coquille sphérique avec un intérieur vide comme le prétend la théorie de la Terre creuse, la gravité terrestre n’agirait sur aucun objet à l’intérieur de cette cavité. Compte tenu de la masse et du volume de la Terre, une cavité terrestre ne peut pas exister, et même s’il y en avait une, les êtres vivants qui s’y trouveraient ne vivraient pas en prenant l’intérieur de la coquille sphérique comme sol, mais flotteraient en état d’apesanteur comme dans une station spatiale.
Des micro-organismes peuvent vivre dans les couches géologiques profondes à quelques kilomètres sous terre, mais au moins pas sous la forme prétendues par la théorie de la Terre creuse. J’aime beaucoup le roman de Jules Verne “Voyage au centre de la Terre” et le film “Journey to the Center of the Earth”, mais il faut apprécier les œuvres de fiction comme des fictions et ne pas les croire sérieusement.

Quand $b<R<a$

\(\begin{align*} \Phi(b<R<a) &= -\frac{4\pi\rho G}{3R}(R^3 - b^3) - 2\pi\rho G(a^2 - R^2) \\ &= -4\pi\rho G \left( \frac{a^2}{2} - \frac{b^3}{3R} - \frac{R^2}{6} \right) \label{eqn:within_spherical_shell}\tag{21} \end{align*}\)

Résultats

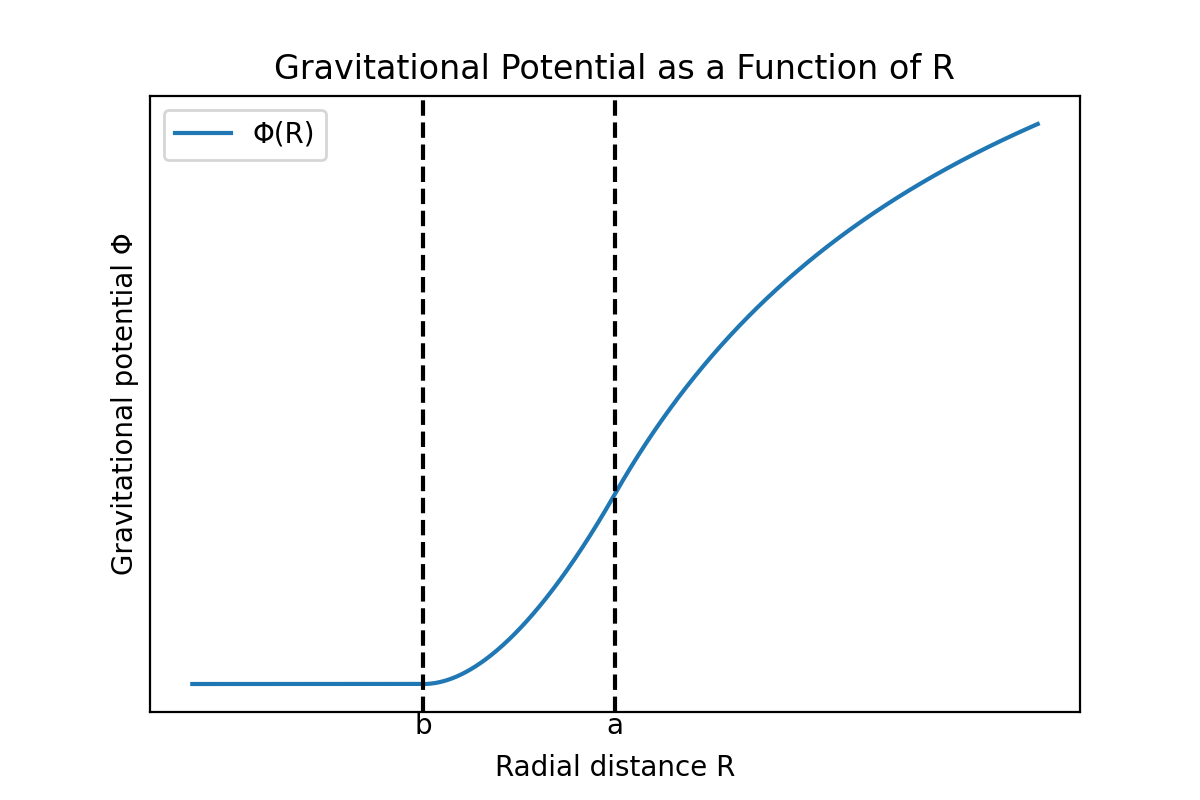
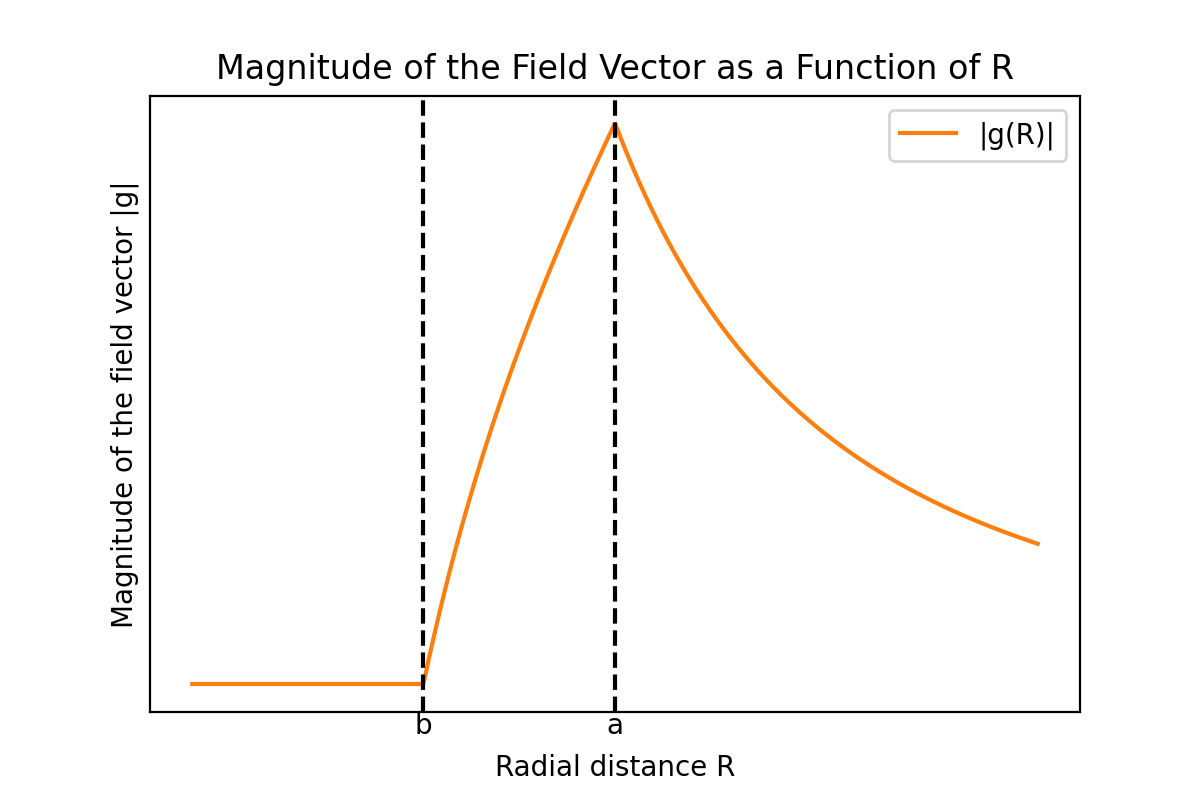
Les graphiques suivants représentent le potentiel gravitationnel $\Phi$ dans les trois régions calculées précédemment, ainsi que la magnitude du vecteur champ gravitationnel correspondant $|\mathbf{g}|$ en fonction de la distance $R$.

• Code de visualisation Python : dépôt yunseo-kim/physics-visualizations
• Licence : Voir ici

On peut voir que le potentiel gravitationnel et la magnitude du vecteur champ gravitationnel sont continus. Si le potentiel gravitationnel était discontinu en un point, le gradient du potentiel en ce point, c’est-à-dire la magnitude de la gravité, deviendrait infini en ce point, ce qui n’est pas physiquement valable, donc la fonction potentielle doit être continue en tous points. Cependant, la dérivée du vecteur champ gravitationnel est discontinue aux surfaces intérieure et extérieure de la coquille.

Exemple : Courbes de rotation galactique

Selon les observations astronomiques, dans de nombreuses galaxies spirales en rotation autour de leur centre, comme notre Voie lactée ou la galaxie d’Andromède, la plupart des masses observables sont concentrées près du centre. Cependant, les vitesses orbitales des masses dans ces galaxies spirales, comme on peut le voir dans le graphique suivant, ne correspondent pas aux valeurs théoriquement prédites à partir de la distribution de masse observable et restent presque constantes au-delà d’une certaine distance.

Source de l’image

• Auteur : utilisateur Wikipedia PhilHibbs
• Licence : Domaine Public

Courbe de rotation de la galaxie spirale M33 (galaxie du Triangle)

• Auteur : utilisateur Wikimedia Mario De Leo
• Licence : CC BY-SA 4.0

Prédisons la vitesse orbitale en fonction de la distance lorsque la masse de la galaxie est concentrée au centre, confirmons que cette prédiction ne correspond pas aux observations, et montrons que la masse $M(R)$ distribuée dans un rayon $R$ du centre galactique doit être proportionnelle à $R$ pour expliquer les résultats observés.

D’abord, si la masse galactique $M$ est concentrée au centre, la vitesse orbitale à la distance $R$ est :

\[\frac{GMm}{R^2} = \frac{mv^2}{R}\] \[v = \sqrt{\frac{GM}{R}} \propto \frac{1}{\sqrt{R}}.\]

Dans ce cas, on prédit une vitesse orbitale décroissant en $1/\sqrt{R}$ comme indiqué par les lignes pointillées dans les deux graphiques ci-dessus, mais selon les observations, la vitesse orbitale $v$ reste presque constante indépendamment de la distance $R$, donc la prédiction ne correspond pas aux observations. Ces résultats observationnels ne peuvent être expliqués que si $M(R)\propto R$.

En posant $M(R) = kR$ avec une constante de proportionnalité $k$ :

\[v = \sqrt{\frac{GM(R)}{R}} = \sqrt{Gk}\ \text{(constante)}.\]

De ceci, les astrophysiciens concluent qu’il doit y avoir de la “matière noire” non découverte dans de nombreuses galaxies, et que cette matière noire doit représenter plus de 90% de la masse de l’univers. Cependant, l’identité de la matière noire n’a pas encore été clairement élucidée, et bien que ce ne soit pas la théorie dominante, il existe des tentatives comme la dynamique newtonienne modifiée (Modified Newtonian Dynamics, MOND) qui essaient d’expliquer les résultats observés sans supposer l’existence de matière noire. Aujourd’hui, ces domaines de recherche sont à la pointe de l’astrophysique.