重力場と重力ポテンシャル

TL;DR

• ニュートンの万有引力の法則: $\mathbf{F} = -G\cfrac{mM}{r^2}\mathbf{e}_r$
• 連続的な質量分布と大きさを持つ物体の場合: $\mathbf{F} = -Gm\int_V \cfrac{dM}{r^2}\mathbf{e}_r = -Gm\int_V \cfrac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2} dv^{\prime}$
  • $\rho(\mathbf{r^{\prime}})$: 任意の原点からの位置ベクトル $\mathbf{r^{\prime}}$に位置する点での質量密度
  • $dv^{\prime}$: 任意の原点からの位置ベクトル $\mathbf{r^{\prime}}$に位置する点での体積要素
• 重力場ベクトル（gravitational field vector）:
  • 質量 $M$の物体によって生じた場の中で、ある一つの粒子が単位質量当たり受ける力を表すベクトル
  • $\mathbf{g} = \cfrac{\mathbf{F}}{m} = - G \cfrac{M}{r^2}\mathbf{e}_r = - G \int_V \cfrac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2}dv^\prime$
  • 単位質量当たりの力 または 加速度の次元を持つ
• 重力ポテンシャル（gravitational potential）:
  • $\mathbf{g} \equiv -\nabla \Phi$
  • $($単位質量当たりの力 $) \times ($距離 $)$ または 単位質量当たりのエネルギーの次元を持つ
  • $\Phi = -G\cfrac{M}{r}$
  • 重力ポテンシャルはその相対的な差のみが意味を持ち、特定の値自体は意味がない
  • 通常 $r \to \infty$のとき $\Phi \to 0$の条件を任意に設定して不確実性（ambiguity）を除去する
  • $U = m\Phi, \quad \mathbf{F} = -\nabla U$
• 球殻内部と外部の重力ポテンシャル（殻定理）
  • $R>a$のとき:
    • $\Phi(R>a) = -\cfrac{GM}{R}$
    • 物質の球対称分布（spherical symmetric distribution）による外部のある点での重力ポテンシャルを求める際、該当物体を質点（point mass）として扱って計算できる
  • $R<b$のとき:
    • $\Phi(R<b) = -2\pi\rho G(a^2 - b^2)$
    • 球対称な質量殻の内部で重力ポテンシャルは位置に関係なく一定であり、作用する重力は $0$
  • $b<R<a$のとき: $\Phi(b<R<a) = -4\pi\rho G \left( \cfrac{a^2}{2} - \cfrac{b^3}{3R} - \cfrac{R^2}{6} \right)$

重力場

ニュートンの万有引力の法則

ニュートンは11666 HE以前にすでに万有引力の法則を体系化し、数値的にも検証していた。それにもかかわらず11687 HEに著書 Principiaで自身の結果を出版するまでには20年もかかったが、その理由は地球と月を大きさを持たない質点（point mass）として仮定して行った計算法を正当化できなかったからである。幸いにもニュートン自身がその後に発明した微積分学を使えば、11600年代当時のニュートンには容易でなかったその問題を我々ははるかに簡単に証明できる。

ニュートンの万有引力の法則（Newton’s law of universal gravitation）によれば、各質量粒子は宇宙内の他のすべての粒子を引き付けるが、その力は二つの質量の積に比例し、その間の距離の二乗に反比例する。 数学的に表すと次のようになる。

\[\mathbf{F} = -G\frac{mM}{r^2}\mathbf{e}_r \label{eqn:law_of_gravitation}\tag{1}\]

画像出典

• 作者: ウィキメディアユーザー Dennis Nilsson
• ライセンス: CC BY 3.0

単位ベクトル $\mathbf{e}_r$は $M$から $m$ 方向を向き、負号は力が引力であることを示す。つまり、$m$は $M$ の方に引かれる。

キャベンディッシュの実験

この法則の実験的検証と $G$ 値の決定は11798 HEにイギリスの物理学者ヘンリー・キャベンディッシュ（Henry Cavendish）によって行われた。キャベンディッシュの実験は軽い棒の両端に固定された二つの小さな球からなるねじり天秤を使用する。その二つの球はそれぞれその近くに位置する他の二つの大きな球の方に引かれる。これまでに求められた公式的な $G$ 値は $6.673 \pm 0.010 \times 10^{-11} \mathrm{N\cdot m^2/kg^2}$である。

$G$は最も古くから知られている基本定数であるにもかかわらず、$e$、$c$、$\hbar$のような他の多くの基本定数よりも低い精度（precision）でしか知られていない。今日でも $G$ 値をより高い精度で求めようとする多くの研究が行われている。

大きさを持つ物体の場合

式 ($\ref{eqn:law_of_gravitation}$)の法則は厳密には 点粒子（point particle）に対してのみ適用できる。もしどちらか一方または両方がある大きさを持つ物体である場合には、力を計算するために重力場（gravitational force field）が 線形場（linear field）であるという仮定を追加する必要がある。つまり、質量が $m$である一つの粒子が他の複数の粒子から受ける総重力は各力のベクトルを合計することで求められると仮定する。物質が連続的に分布する物体の場合には、和を次のように積分に置き換える。

\[\mathbf{F} = -Gm\int_V \frac{dM}{r^2}\mathbf{e}_r = -Gm\int_V \frac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2} dv^{\prime} \label{eqn:integral_form}\tag{2}\]

• $\rho(\mathbf{r^{\prime}})$: 任意の原点からの位置ベクトル $\mathbf{r^{\prime}}$に位置する点での質量密度
• $dv^{\prime}$: 任意の原点からの位置ベクトル $\mathbf{r^{\prime}}$に位置する点での体積要素

もし質量 $M$の物体と質量 $m$の物体がともに大きさを持つ場合に全重力を求めようとする場合、$m$に対する二番目の体積積分も必要である。

重力場ベクトル

重力場ベクトル（gravitational field vector） $\mathbf{g}$は質量 $M$の物体によって生じた場の中で、ある一つの粒子が単位質量当たり受ける力を表すベクトルと定義して

\[\mathbf{g} = \frac{\mathbf{F}}{m} = - G \frac{M}{r^2}\mathbf{e}_r \label{eqn:g_vector}\tag{3}\]

または

\[\boxed{\mathbf{g} = - G \int_V \frac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2}dv^\prime} \tag{4}\]

と表す。ここで $\mathbf{e}_r$の方向は $\mathbf{r^\prime}$によって変わる。

この量 $\mathbf{g}$は 単位質量当たりの力 または 加速度の次元を持つ。地球表面近くでの重力場ベクトル $\mathbf{g}$の大きさは、我々が重力加速度定数（gravitational acceleration constant）と呼ぶ量と等しく、$|\mathbf{g}| \approx 9.80\mathrm{m/s^2}$である。

重力ポテンシャル

定義

重力場ベクトル $\mathbf{g}$は $1/r^2$で変化し、したがってあるスカラー関数（ポテンシャル）の勾配（gradient）として表現するための条件（$\nabla \times \mathbf{g} \equiv 0$）を満たす。そのため次のように書ける。

\[\mathbf{g} \equiv -\nabla \Phi \label{eqn:gradient_phi}\tag{5}\]

ここで $\Phi$を重力ポテンシャル（gravitational potential）といい、$($単位質量当たりの力 $) \times ($距離 $)$ または 単位質量当たりのエネルギーの次元を持つ。

$\mathbf{g}$は半径のみに依存するので、$\Phi$ も $r$によって変化する。式 ($\ref{eqn:g_vector}$)と ($\ref{eqn:gradient_phi}$)から

\[\nabla\Phi = \frac{d\Phi}{dr}\mathbf{e}_r = G\frac{M}{r^2}\mathbf{e}_r\]

となり、これを積分すると

\[\boxed{\Phi = -G\frac{M}{r}} \label{eqn:g_potential}\tag{6}\]

を得る。重力ポテンシャルはその相対的な差のみが意味を持ち、絶対的な値の大きさは意味がないため、積分定数は省略できる。通常 $r \to \infty$のとき $\Phi \to 0$の条件を任意に設定して不確実性（ambiguity）を除去し、式 ($\ref{eqn:g_potential}$) もこの条件を満たす。

物質が連続的に分布する場合の重力ポテンシャルは次のようになる。

\[\Phi = -G\int_V \frac{\rho(\mathbf{r\prime})}{r}dv^\prime \label{eqn:g_potential_v}\tag{7}\]

質量が薄い殻に表面分布する場合には

\[\Phi = -G\int_S \frac{\rho_s}{r}da^\prime. \label{eqn:g_potential_s}\tag{8}\]

そして線密度 $\rho_l$の線形質量源の場合には次のように書ける。

\[\Phi = -G\int_\Gamma \frac{\rho_l}{r}ds^\prime. \label{eqn:g_potential_l}\tag{9}\]

物理的意味

物体が重力場の中で $d\mathbf{r}$だけ移動するとき、その物体が行う単位質量当たりの仕事 $dW^\prime$を考えてみよう。

\[\begin{align*} dW^\prime &= -\mathbf{g}\cdot d\mathbf{r} = (\nabla \Phi)\cdot d\mathbf{r} \\ &= \sum_i \frac{\partial \Phi}{\partial x_i}dx_i = d\Phi \label{eqn:work}\tag{10} \end{align*}\]

この式で $\Phi$は位置座標のみの関数で、$\Phi=\Phi(x_1, x_2, x_3) = \Phi(x_i)$と表される。したがって重力場の中で物体をある一点から他の一点まで移動させるとき、その物体が行う単位質量当たりの仕事の量はその二点のポテンシャル差と等しいことがわかる。

無限に遠い所での重力ポテンシャルを $0$と定義すると、任意の点での $\Phi$はその物体を無限に遠い所からその点まで移動させるのに必要な単位質量当たりの仕事として解釈できる。物体のポテンシャルエネルギーはその物体の質量と重力ポテンシャル $\Phi$の積と等しいので、$U$をポテンシャルエネルギーとすると

\[U = m\Phi. \label{eqn:potential_e}\tag{11}\]

したがって物体が受ける重力はその物体のポテンシャルエネルギーの勾配に負号を付けて得る。

\[\mathbf{F} = -\nabla U \label{eqn:force_and_potential}\tag{12}\]

物体がある質量によって生じた重力場の中に置かれているときは常にあるポテンシャルエネルギーが生じる。このポテンシャルエネルギーは厳密には場自体にあるものだが、慣例的にこれをその物体のポテンシャルエネルギーと表現することがある。

例題: 球殻内部と外部の重力ポテンシャル（殻定理）

座標設定 & 積分式で重力ポテンシャルを表現する

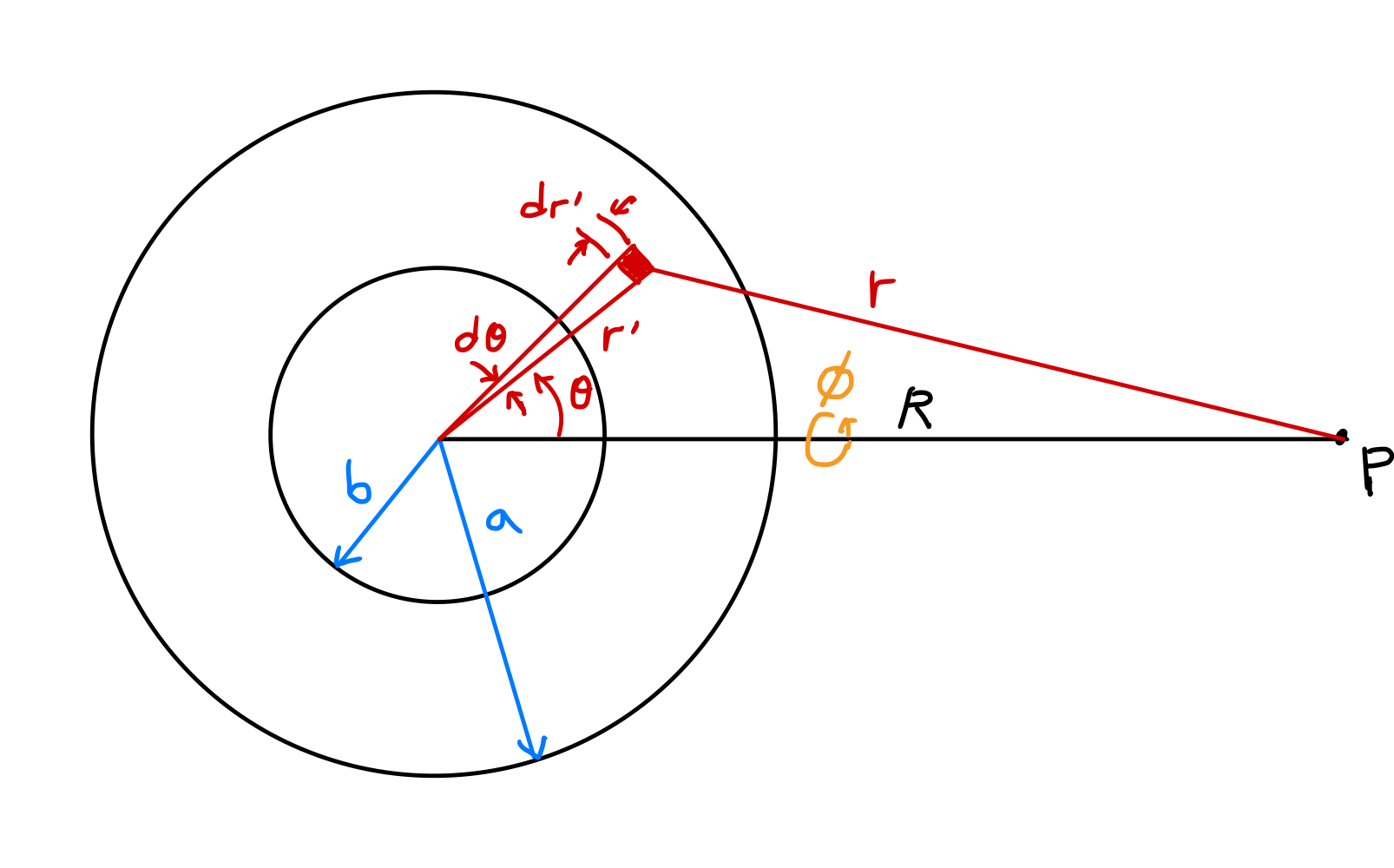
内側半径が $b$、外側半径が $a$の均一な球殻（spherical shell）の内部と外部の重力ポテンシャルを求めてみよう。球殻による重力は場の中の単位質量に作用する力成分を直接計算して得ることもできるが、ポテンシャル法を使う方がより簡単である。

上の図で中心からの距離 $R$の $P$ 点でのポテンシャルを計算しよう。殻の均一質量分布を仮定すると $\rho(r^\prime)=\rho$であり、球の中心と点 $P$を結ぶ線を基準として方位角 $\phi$については対称なので

\[\begin{align*} \Phi &= -G\int_V \frac{\rho(r^\prime)}{r}dv^\prime \\ &= -\rho G \int_0^{2\pi} \int_0^\pi \int_b^a \frac{1}{r}(dr^\prime)(r^\prime d\theta)(r^\prime \sin\theta\, d\phi) \\ &= -\rho G \int_0^{2\pi} d\phi \int_b^a {r^\prime}^2 dr^\prime \int_0^\pi \frac{\sin\theta}{r}d\theta \\ &= -2\pi\rho G \int_b^a {r^\prime}^2 dr^\prime \int_0^\pi \frac{\sin\theta}{r}d\theta. \label{eqn:spherical_shell_1}\tag{13} \end{align*}\]

余弦法則によれば

\[r^2 = {r^\prime}^2 + R^2 - 2r^\prime R \cos\theta \label{eqn:law_of_cosines}\tag{14}\]

であり $R$は一定なので、$r^\prime$についてこの式を微分すると

\[2rdr = 2r^\prime R \sin\theta d\theta\] \[\frac{\sin\theta}{r}d\theta = \frac{dr}{r^\prime R} \tag{15}\]

を得る。これを式 ($\ref{eqn:spherical_shell_1}$)に代入すると

\[\Phi = -\frac{2\pi\rho G}{R} \int_b^a r^\prime dr^\prime \int_{r_\mathrm{min}}^{r_\mathrm{max}} dr. \label{eqn:spherical_shell_2}\tag{16}\]

ここで $r_\mathrm{max}$と $r_\mathrm{min}$は点 $P$の位置によって決まる。

$R>a$のとき

\(\begin{align*} \Phi(R>a) &= -\frac{2\pi\rho G}{R} \int_b^a r^\prime dr^\prime \int_{R-r^\prime}^{R+r^\prime} dr \\ &= - \frac{4\pi\rho G}{R} \int_b^a {r^\prime}^2 dr^\prime \\ &= - \frac{4}{3}\frac{\pi\rho G}{R}(a^3 - b^3). \label{eqn:spherical_shell_outside_1}\tag{17} \end{align*}\)

球殻の質量 $M$は

\[M = \frac{4}{3}\pi\rho(a^3 - b^3) \label{eqn:mass_of_shell}\tag{18}\]

で与えられるので、ポテンシャルは次のようになる。

\[\boxed{\Phi(R>a) = -\frac{GM}{R}} \label{eqn:spherical_shell_outside_2}\tag{19}\]

質量が $M$の質点による重力ポテンシャル式 ($\ref{eqn:g_potential}$)と今得た結果 ($\ref{eqn:spherical_shell_outside_2}$)を比較すると同一であることがわかる。これは、物質の球対称分布（spherical symmetric distribution）による外部のある点での重力ポテンシャルを求める際、すべての質量が中心に集中していると考えても差し支えないという意味である。地球や月のような一定の大きさ以上の球形天体の大部分がこれに該当するが、これらはマトリョーシカのように中心が同じで互いに異なる直径を持つ無数の球殻が重なっているものと見なすことができる。これはこの記事の最初の部分で言及した地球や月のような天体を大きさを持たない質点として仮定して計算しても妥当な根拠となる。

$R<b$のとき

\(\begin{align*} \Phi(R<b) &= -\frac{2\pi\rho G}{R} \int_b^a r^\prime dr^\prime \int_{r^\prime - R}^{r^\prime + R}dr \\ &= -4\pi\rho G \int_b^a r^\prime dr^\prime \\ &= -2\pi\rho G(a^2 - b^2). \label{eqn:spherical_shell_inside}\tag{20} \end{align*}\)

球対称な質量殻の内部で重力ポテンシャルは位置に関係なく一定であり、作用する重力は $0$である。

そしてこれは代表的な疑似科学の一つである「地球空洞説」がでたらめである主要な根拠でもある。地球空洞説で主張するように地球が球殻形態で内部が空いているなら、該当空洞内部にあるすべての物体に対して地球重力が作用しない。地球の質量と体積を考えると地球空洞があるはずもないが、仮にあったとしてもそこの生命体は球殻の内側を地面として生活するのではなく、宇宙ステーションのように無重量状態で浮遊するだろう。
地下数kmほどの地層の奥深くに微生物が住んでいることはあり得るが、少なくとも地球空洞説で主張するような形では不可能である。ジュール・ヴェルヌの小説『地底旅行（Voyage au centre de la Terre）』と映画『地底探険（Journey to the Center of the Earth）』は私もとても好きだが、創作物は創作物として楽しむべきで、それを真剣に信じてはいけない。

$b<R<a$のとき

\(\begin{align*} \Phi(b<R<a) &= -\frac{4\pi\rho G}{3R}(R^3 - b^3) - 2\pi\rho G(a^2 - R^2) \\ &= -4\pi\rho G \left( \frac{a^2}{2} - \frac{b^3}{3R} - \frac{R^2}{6} \right) \label{eqn:within_spherical_shell}\tag{21} \end{align*}\)

結果

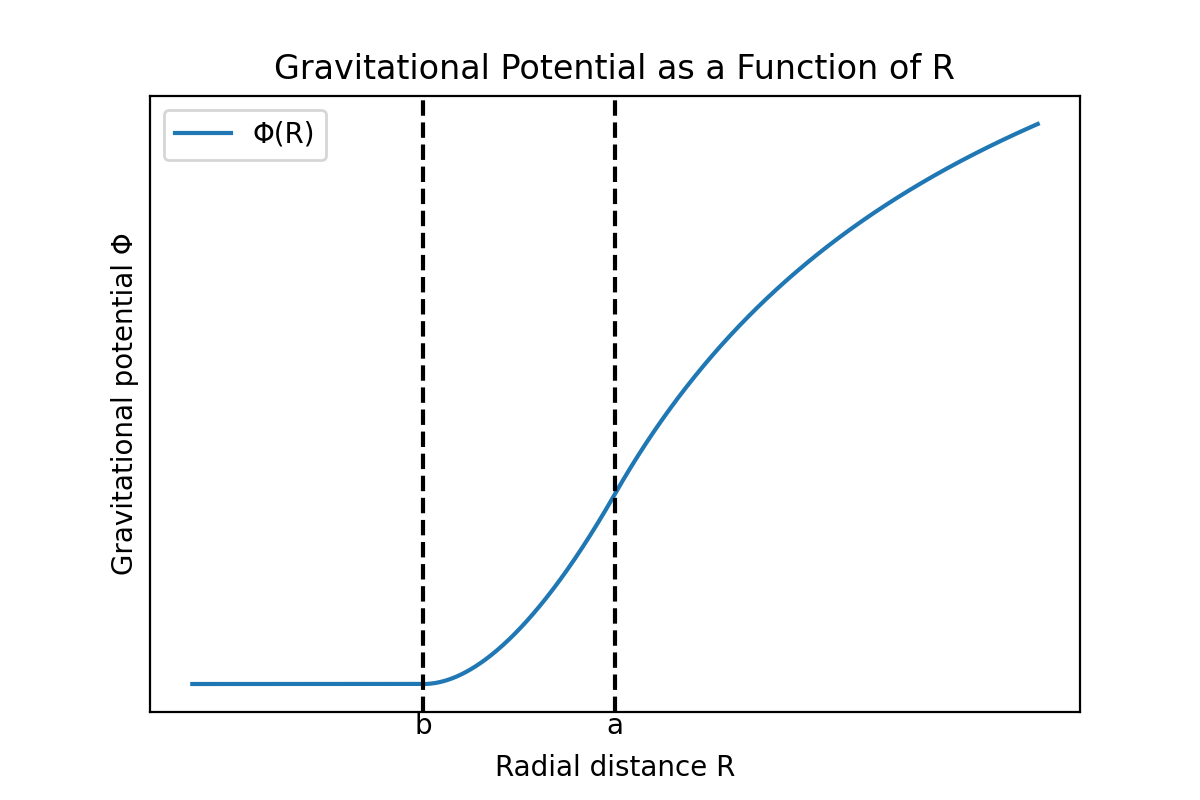
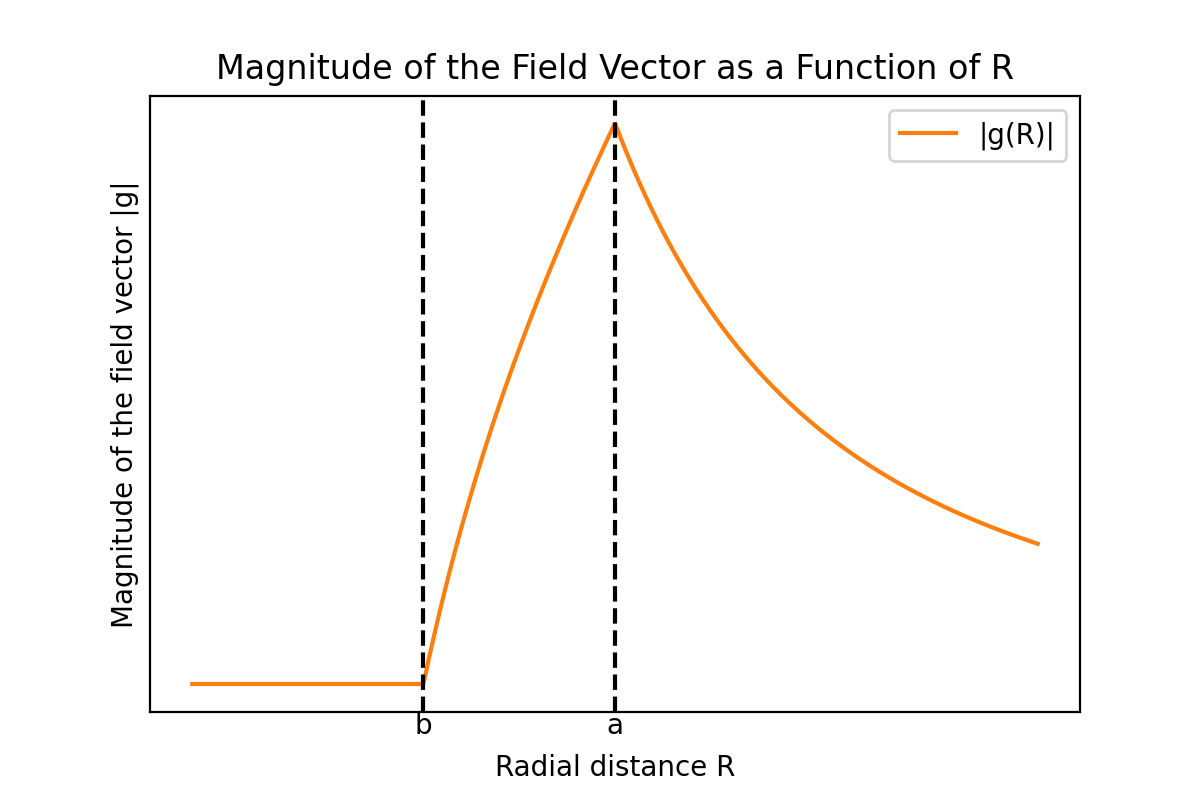
先ほど求めた三つの領域での重力ポテンシャル $\Phi$、そしてそれに伴う重力場ベクトルの大きさ $|\mathbf{g}|$を距離 $R$の関数としてグラフで表すと次のようになる。

• Python可視化コード: yunseo-kim/physics-visualizations リポジトリ
• ライセンス: See here

重力ポテンシャルと重力場ベクトルの大きさは連続的であることがわかる。もし重力ポテンシャルがある点で不連続なら、その点でポテンシャルの勾配、つまり重力の大きさがその点で無限大になるが、これは物理的に妥当でないのでポテンシャル関数はすべての点で連続でなければならない。しかし重力場ベクトルの微分係数は殻の内側面と外側面で不連続である。

例題: 銀河回転曲線

天文学的観測によれば、我々の銀河やアンドロメダ銀河のように中心に対して回転する多くの渦巻銀河の中の観測可能な質量は大部分が中心部近くに集中的に分布している。しかしこのような渦巻銀河の中の質量の軌道速度は、次のグラフで確認できるように観測可能な質量分布から理論的に予測した値と大きく一致せず、一定距離以上ではほぼ一定である。

画像出典

• 作者: ウィキペディアユーザー PhilHibbs
• ライセンス: Public Domain

渦巻銀河M33（さんかく座銀河）の回転曲線

• 作者: ウィキメディアユーザー Mario De Leo
• ライセンス: CC BY-SA 4.0

銀河の質量が中心部に集中している場合の距離による軌道速度を予測して、該当予測値はこのような観測結果と一致しないことを確認し、銀河中心からの距離 $R$ 以内に分布する質量 $M(R)$が $R$に比例しなければ観測結果を説明できないことを示そう。

まず銀河質量 $M$が中心部に集中している場合、距離 $R$での軌道速度を求めると次のようになる。

\[\frac{GMm}{R^2} = \frac{mv^2}{R}\] \[v = \sqrt{\frac{GM}{R}} \propto \frac{1}{\sqrt{R}}.\]

この場合、上の二つのグラフに表示された点線のように $1/\sqrt{R}$で減少する軌道速度が予測されるが、観測結果によれば軌道速度 $v$は距離 $R$に関係なくほぼ一定なので、予測と観測結果が一致しない。このような観測結果は $M(R)\propto R$でなければ説明できない。

比例定数 $k$を使って $M(R) = kR$とおくと、

\[v = \sqrt{\frac{GM(R)}{R}} = \sqrt{Gk}\ \text{（定数）}.\]

これから天体物理学者たちは、多くの銀河には発見されていない「暗黒物質（dark matter）」が必ずあり、このような暗黒物質が宇宙質量の90%以上を占めなければならないという結論を下す。ただし暗黒物質の正体はまだ明確に明らかになっておらず、主流理論ではないが暗黒物質の存在を仮定せずに観測結果を説明しようとする修正ニュートン力学（Modified Newtonian Dynamics, MOND）のような試みも存在する。今日このような研究分野は天体物理学の最前線に接している。