重力場與重力位勢

TL;DR

• 牛頓萬有引力定律：$\mathbf{F} = -G\cfrac{mM}{r^2}\mathbf{e}_r$
• 連續質量分布且具有大小的物體情況：$\mathbf{F} = -Gm\int_V \cfrac{dM}{r^2}\mathbf{e}_r = -Gm\int_V \cfrac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2} dv^{\prime}$
  • $\rho(\mathbf{r^{\prime}})$：從任意原點到位置向量 $\mathbf{r^{\prime}}$ 處的質量密度
  • $dv^{\prime}$：從任意原點到位置向量 $\mathbf{r^{\prime}}$ 處的體積元素
• 重力場向量（gravitational field vector）：
  • 表示質量 $M$ 的物體所產生的場中，某一粒子每單位質量所受的力的向量
  • $\mathbf{g} = \cfrac{\mathbf{F}}{m} = - G \cfrac{M}{r^2}\mathbf{e}_r = - G \int_V \cfrac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2}dv^\prime$
  • 具有每單位質量的力或加速度的量綱
• 重力位勢（gravitational potential）：
  • $\mathbf{g} \equiv -\nabla \Phi$
  • 具有（每單位質量的力）×（距離）或每單位質量的能量的量綱
  • $\Phi = -G\cfrac{M}{r}$
  • 重力位勢只有相對差值才有意義，特定值本身沒有意義
  • 通常設定 $r \to \infty$ 時 $\Phi \to 0$ 的條件來消除不確定性（ambiguity）
  • $U = m\Phi, \quad \mathbf{F} = -\nabla U$
• 球殼內部與外部的重力位勢（殼層定理）
  • $R>a$ 時：
    • $\Phi(R>a) = -\cfrac{GM}{R}$
    • 計算物質球對稱分布（spherical symmetric distribution）對外部某點的重力位勢時，可將該物體視為質點（point mass）來計算
  • $R<b$ 時：
    • $\Phi(R<b) = -2\pi\rho G(a^2 - b^2)$
    • 在球對稱質量殼層內，重力位勢與位置無關且為常數，作用的重力為 $0$
  • $b<R<a$ 時：$\Phi(b<R<a) = -4\pi\rho G \left( \cfrac{a^2}{2} - \cfrac{b^3}{3R} - \cfrac{R^2}{6} \right)$

重力場

牛頓萬有引力定律

牛頓在 11666 HE 之前就已經系統化了萬有引力定律並進行了數值驗證。儘管如此，直到 11687 HE 才在著作《原理》（Principia）中發表他的結果，又花了 20 年的時間，原因是無法證明將地球和月球假設為沒有大小的質點（point mass）進行計算的合理性。幸運的是，使用牛頓後來發明的微積分學，我們可以比當時的牛頓更容易地證明這個問題。

根據牛頓萬有引力定律（Newton’s law of universal gravitation），每個質量粒子都會吸引宇宙中的其他所有粒子，該力與兩個質量的乘積成正比，與它們之間距離的平方成反比。 數學表示如下：

\[\mathbf{F} = -G\frac{mM}{r^2}\mathbf{e}_r \label{eqn:law_of_gravitation}\tag{1}\]

圖片來源

• 作者：維基媒體用戶 Dennis Nilsson
• 授權：CC BY 3.0

單位向量 $\mathbf{e}_r$ 指向從 $M$ 到 $m$ 的方向，負號表示力為引力。也就是說，$m$ 被拉向 $M$。

卡文迪許實驗

這個定律的實驗驗證和 $G$ 值的測定是在 11798 HE 由英國物理學家亨利·卡文迪許（Henry Cavendish）完成的。卡文迪許實驗使用扭轉天平，該天平由固定在輕桿兩端的兩個小球組成。這兩個球分別被附近的另外兩個大球吸引。目前得到的官方 $G$ 值為 $6.673 \pm 0.010 \times 10^{-11} \mathrm{N\cdot m^2/kg^2}$。

儘管 $G$ 是最早為人所知的基本常數，但其精確度（precision）卻比 $e$、$c$、$\hbar$ 等大多數其他基本常數要低。即使在今天，仍有許多研究試圖以更高的精確度測定 $G$ 值。

具有大小的物體情況

式 ($\ref{eqn:law_of_gravitation}$) 的定律嚴格來說只能適用於點粒子（point particle）。如果其中一方或雙方都是具有某種大小的物體，則需要額外假設重力場（gravitational force field）是線性場（linear field）來計算力。也就是說，假設質量為 $m$ 的一個粒子從其他多個粒子受到的總重力可以通過各個力的向量相加來求得。對於物質連續分布的物體，將求和改為如下積分：

\[\mathbf{F} = -Gm\int_V \frac{dM}{r^2}\mathbf{e}_r = -Gm\int_V \frac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2} dv^{\prime} \label{eqn:integral_form}\tag{2}\]

• $\rho(\mathbf{r^{\prime}})$：從任意原點到位置向量 $\mathbf{r^{\prime}}$ 處的質量密度
• $dv^{\prime}$：從任意原點到位置向量 $\mathbf{r^{\prime}}$ 處的體積元素

如果質量 $M$ 的物體和質量 $m$ 的物體都具有大小，要求得總重力時還需要對 $m$ 進行第二次體積積分。

重力場向量

重力場向量（gravitational field vector） $\mathbf{g}$ 定義為質量 $M$ 的物體所產生的場中，某一粒子每單位質量所受的力的向量：

\[\mathbf{g} = \frac{\mathbf{F}}{m} = - G \frac{M}{r^2}\mathbf{e}_r \label{eqn:g_vector}\tag{3}\]

或

\[\boxed{\mathbf{g} = - G \int_V \frac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2}dv^\prime} \tag{4}\]

這裡 $\mathbf{e}_r$ 的方向隨 $\mathbf{r^\prime}$ 而變化。

這個量 $\mathbf{g}$ 具有每單位質量的力或加速度的量綱。地球表面附近的重力場向量 $\mathbf{g}$ 的大小就是我們稱為重力加速度常數（gravitational acceleration constant）的量，$|\mathbf{g}| \approx 9.80\mathrm{m/s^2}$。

重力位勢

定義

重力場向量 $\mathbf{g}$ 以 $1/r^2$ 變化，因此滿足表示為某個標量函數（位勢）梯度（gradient）的條件（$\nabla \times \mathbf{g} \equiv 0$）。所以可以寫成：

\[\mathbf{g} \equiv -\nabla \Phi \label{eqn:gradient_phi}\tag{5}\]

這裡 $\Phi$ 稱為重力位勢（gravitational potential），具有（每單位質量的力）×（距離）或每單位質量的能量的量綱。

由於 $\mathbf{g}$ 只依賴於半徑，$\Phi$ 也隨 $r$ 變化。從式 ($\ref{eqn:g_vector}$) 和 ($\ref{eqn:gradient_phi}$) 得到：

\[\nabla\Phi = \frac{d\Phi}{dr}\mathbf{e}_r = G\frac{M}{r^2}\mathbf{e}_r\]

積分後得到：

\[\boxed{\Phi = -G\frac{M}{r}} \label{eqn:g_potential}\tag{6}\]

由於重力位勢只有相對差值才有意義，絕對值的大小沒有意義，所以可以省略積分常數。通常設定 $r \to \infty$ 時 $\Phi \to 0$ 的條件來消除不確定性（ambiguity），式 ($\ref{eqn:g_potential}$) 也滿足這個條件。

物質連續分布時的重力位勢如下：

\[\Phi = -G\int_V \frac{\rho(\mathbf{r\prime})}{r}dv^\prime \label{eqn:g_potential_v}\tag{7}\]

質量在薄殼表面分布時：

\[\Phi = -G\int_S \frac{\rho_s}{r}da^\prime. \label{eqn:g_potential_s}\tag{8}\]

線密度為 $\rho_l$ 的線性質量源情況下可以寫成：

\[\Phi = -G\int_\Gamma \frac{\rho_l}{r}ds^\prime. \label{eqn:g_potential_l}\tag{9}\]

物理意義

考慮物體在重力場中移動 $d\mathbf{r}$ 時該物體所做的每單位質量的功 $dW^\prime$：

\[\begin{align*} dW^\prime &= -\mathbf{g}\cdot d\mathbf{r} = (\nabla \Phi)\cdot d\mathbf{r} \\ &= \sum_i \frac{\partial \Phi}{\partial x_i}dx_i = d\Phi \label{eqn:work}\tag{10} \end{align*}\]

在這個式子中，$\Phi$ 只是位置坐標的函數，表示為 $\Phi=\Phi(x_1, x_2, x_3) = \Phi(x_i)$。因此可以知道，在重力場中將物體從某一點移動到另一點時該物體所做的每單位質量的功等於這兩點的位勢差。

如果將無限遠處的重力位勢定義為 $0$，則任意點的 $\Phi$ 可以解釋為將該物體從無限遠處移動到該點所需的每單位質量的功。物體的位勢能等於該物體的質量與重力位勢 $\Phi$ 的乘積，所以設 $U$ 為位勢能時：

\[U = m\Phi. \label{eqn:potential_e}\tag{11}\]

因此，物體受到的重力是該物體位勢能的梯度加上負號得到的：

\[\mathbf{F} = -\nabla U \label{eqn:force_and_potential}\tag{12}\]

當物體處於某個質量產生的重力場中時，總是會產生某種位勢能。這個位勢能嚴格來說存在於場本身，但習慣上表達為該物體的位勢能。

例題：球殼內部與外部的重力位勢（殼層定理）

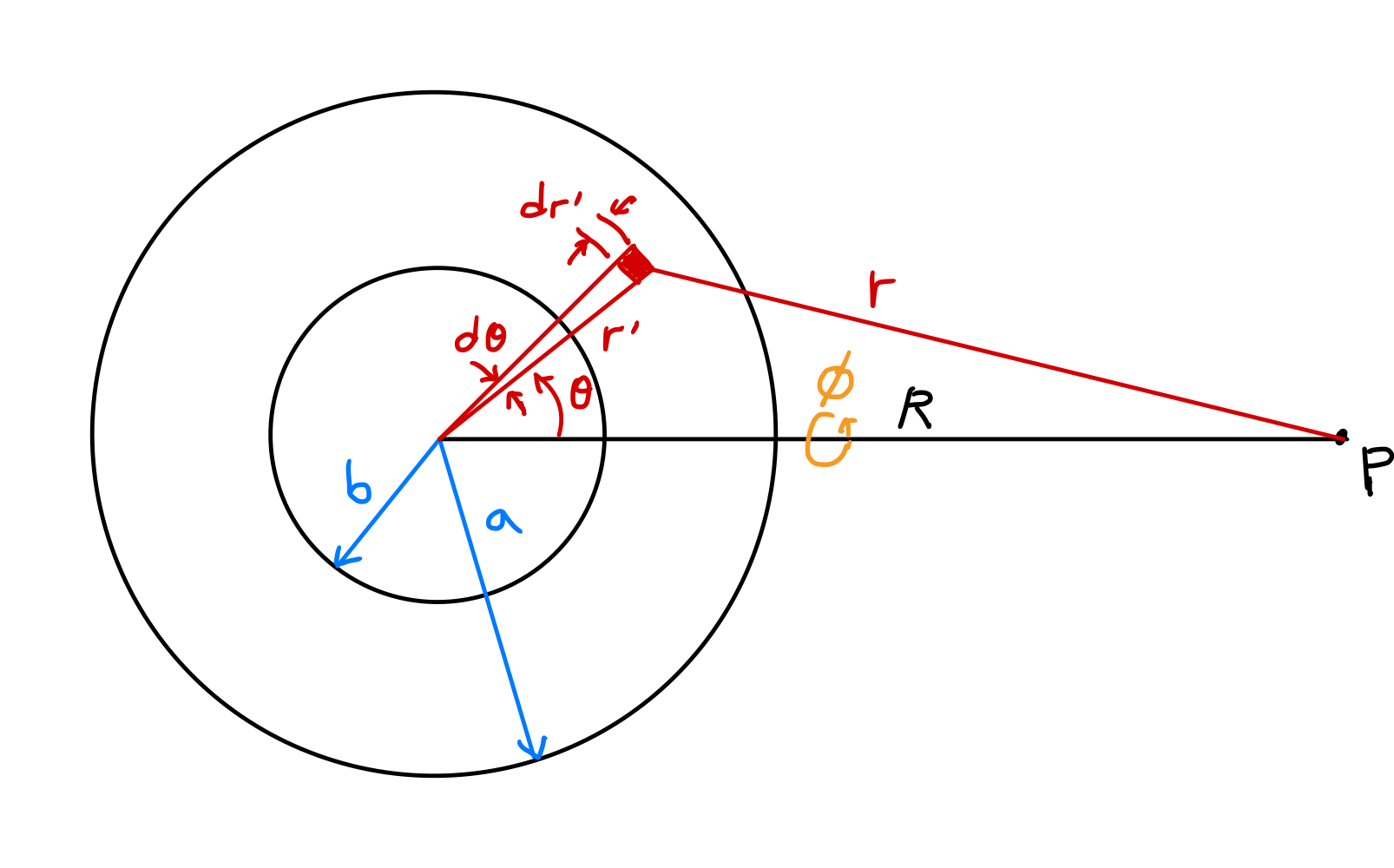
座標設定與用積分式表示重力位勢

求內半徑為 $b$、外半徑為 $a$ 的均勻球殼（spherical shell）內部和外部的重力位勢。球殼產生的重力也可以通過直接計算場中單位質量受到的力分量來得到，但使用位勢方法更簡單。

在上圖中計算距離中心 $R$ 的 $P$ 點的位勢。假設殼層的均勻質量分布，則 $\rho(r^\prime)=\rho$，且相對於連接球心和點 $P$ 的線，對方位角 $\phi$ 對稱，所以：

\[\begin{align*} \Phi &= -G\int_V \frac{\rho(r^\prime)}{r}dv^\prime \\ &= -\rho G \int_0^{2\pi} \int_0^\pi \int_b^a \frac{1}{r}(dr^\prime)(r^\prime d\theta)(r^\prime \sin\theta\, d\phi) \\ &= -\rho G \int_0^{2\pi} d\phi \int_b^a {r^\prime}^2 dr^\prime \int_0^\pi \frac{\sin\theta}{r}d\theta \\ &= -2\pi\rho G \int_b^a {r^\prime}^2 dr^\prime \int_0^\pi \frac{\sin\theta}{r}d\theta. \label{eqn:spherical_shell_1}\tag{13} \end{align*}\]

根據餘弦定律：

\[r^2 = {r^\prime}^2 + R^2 - 2r^\prime R \cos\theta \label{eqn:law_of_cosines}\tag{14}\]

由於 $R$ 是常數，對 $r^\prime$ 微分這個式子得到：

\[2rdr = 2r^\prime R \sin\theta d\theta\] \[\frac{\sin\theta}{r}d\theta = \frac{dr}{r^\prime R} \tag{15}\]

將此代入式 ($\ref{eqn:spherical_shell_1}$) 得到：

\[\Phi = -\frac{2\pi\rho G}{R} \int_b^a r^\prime dr^\prime \int_{r_\mathrm{min}}^{r_\mathrm{max}} dr. \label{eqn:spherical_shell_2}\tag{16}\]

這裡 $r_\mathrm{max}$ 和 $r_\mathrm{min}$ 根據點 $P$ 的位置確定。

$R>a$ 時

\(\begin{align*} \Phi(R>a) &= -\frac{2\pi\rho G}{R} \int_b^a r^\prime dr^\prime \int_{R-r^\prime}^{R+r^\prime} dr \\ &= - \frac{4\pi\rho G}{R} \int_b^a {r^\prime}^2 dr^\prime \\ &= - \frac{4}{3}\frac{\pi\rho G}{R}(a^3 - b^3). \label{eqn:spherical_shell_outside_1}\tag{17} \end{align*}\)

球殼的質量 $M$ 為：

\[M = \frac{4}{3}\pi\rho(a^3 - b^3) \label{eqn:mass_of_shell}\tag{18}\]

所以位勢為：

\[\boxed{\Phi(R>a) = -\frac{GM}{R}} \label{eqn:spherical_shell_outside_2}\tag{19}\]

比較質量為 $M$ 的質點產生的重力位勢式 ($\ref{eqn:g_potential}$) 和剛得到的結果 ($\ref{eqn:spherical_shell_outside_2}$)，可以發現它們相同。這意味著，計算物質球對稱分布（spherical symmetric distribution）對外部某點的重力位勢時，可以認為所有質量都集中在中心。地球或月球等一定大小以上的球形天體大多屬於這種情況，它們可以視為像俄羅斯套娃一樣，由無數個同心但直徑不同的球殼重疊而成。這就是本文開頭提到的將地球或月球等天體假設為沒有大小的質點進行計算也是合理的根據。

$R<b$ 時

\(\begin{align*} \Phi(R<b) &= -\frac{2\pi\rho G}{R} \int_b^a r^\prime dr^\prime \int_{r^\prime - R}^{r^\prime + R}dr \\ &= -4\pi\rho G \int_b^a r^\prime dr^\prime \\ &= -2\pi\rho G(a^2 - b^2). \label{eqn:spherical_shell_inside}\tag{20} \end{align*}\)

在球對稱質量殼層內，重力位勢與位置無關且為常數，作用的重力為 $0$。

這也是代表性偽科學之一「地球空洞說」是胡說八道的主要根據。如果像地球空洞說主張的那樣，地球是球殼形狀且內部是空的，那麼對於該空洞內部的所有物體，地球重力都不會作用。考慮到地球的質量和體積，地球空洞不可能存在，即使存在，那裡的生命體也不會以球殼內側為地面生活，而是像太空站一樣處於無重力狀態漂浮著。
地下數公里深的地層深處可能有微生物生存，但至少不可能像地球空洞說主張的那種形式。我也很喜歡儒勒·凡爾納的小說《地心遊記》（Voyage au centre de la Terre）和電影《地心歷險記》（Journey to the Center of the Earth），但創作作品就應該當作創作作品來欣賞，不要認真相信。

$b<R<a$ 時

\(\begin{align*} \Phi(b<R<a) &= -\frac{4\pi\rho G}{3R}(R^3 - b^3) - 2\pi\rho G(a^2 - R^2) \\ &= -4\pi\rho G \left( \frac{a^2}{2} - \frac{b^3}{3R} - \frac{R^2}{6} \right) \label{eqn:within_spherical_shell}\tag{21} \end{align*}\)

結果

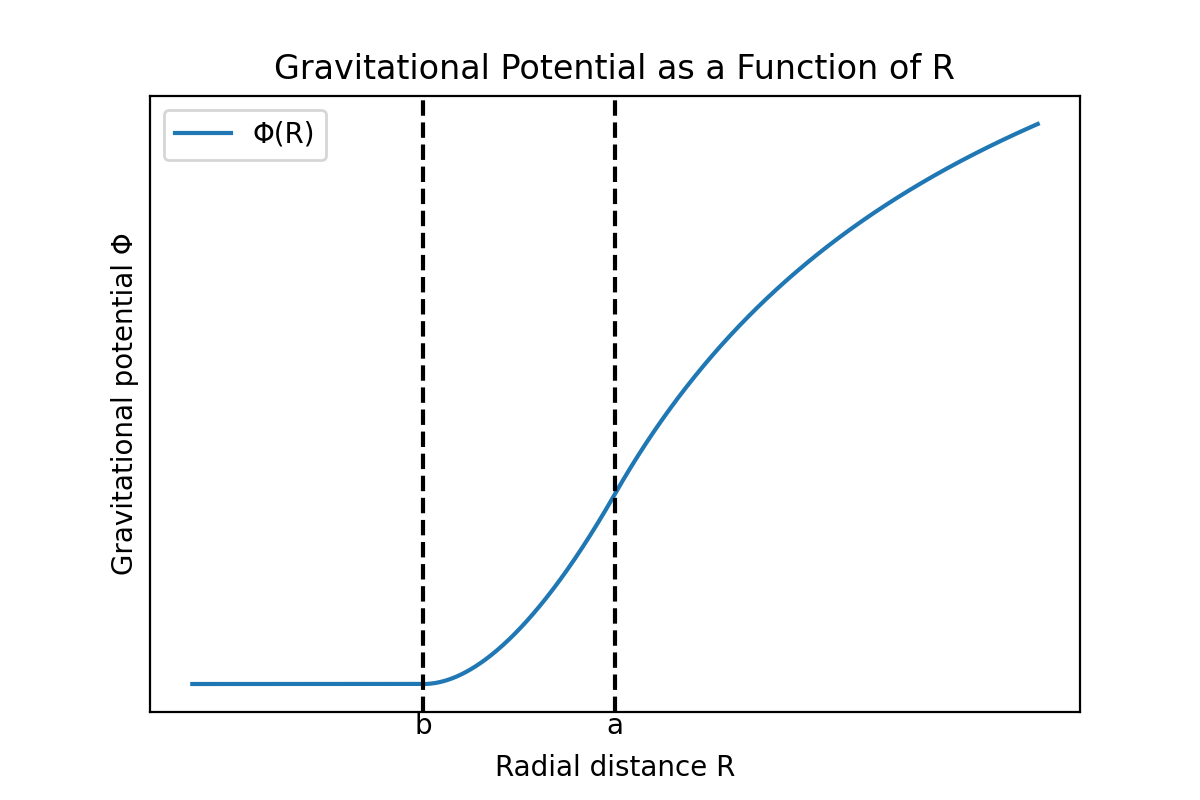
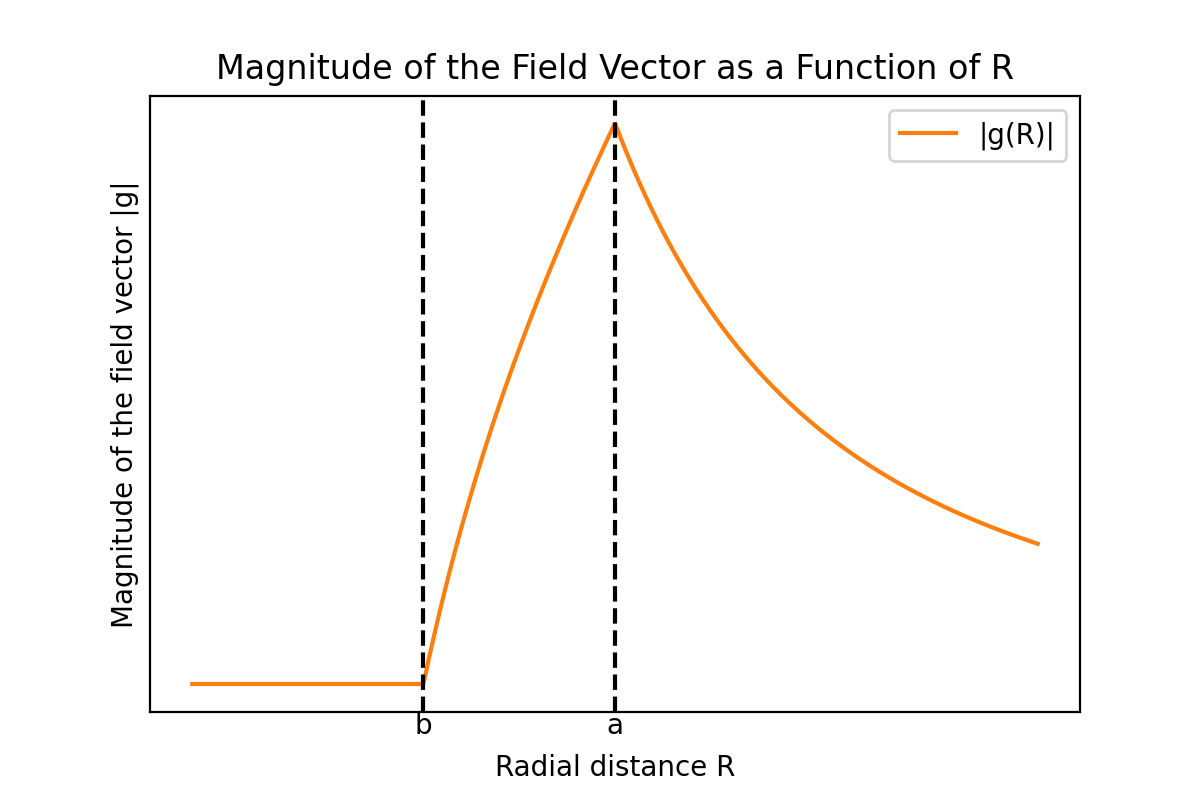
將前面求得的三個區域的重力位勢 $\Phi$ 以及相應的重力場向量大小 $|\mathbf{g}|$ 作為距離 $R$ 的函數用圖表示如下：

• Python 視覺化程式碼：yunseo-kim/physics-visualizations 儲存庫
• 授權：見此處

可以看出重力位勢和重力場向量的大小是連續的。如果重力位勢在某點不連續，那麼該點的位勢梯度，即重力的大小在該點會變成無限大，這在物理上是不合理的，所以位勢函數在所有點都必須連續。但是重力場向量的微分係數在殼層的內表面和外表面處不連續。

例題：星系旋轉曲線

根據天文觀測，在我們銀河系或仙女座星系等圍繞中心旋轉的許多螺旋星系中，可觀測質量大多集中分布在中心部附近。然而，這些螺旋星系中質量的軌道速度如下圖所示，與從可觀測質量分布理論預測的值有很大差異，在一定距離以上幾乎保持恆定。

圖片來源

• 作者：維基百科用戶 PhilHibbs
• 授權：Public Domain

螺旋星系 M33（三角座星系）的旋轉曲線

• 作者：維基媒體用戶 Mario De Leo
• 授權：CC BY-SA 4.0

讓我們預測星系質量集中在中心部時隨距離變化的軌道速度，確認該預測值與這種觀測結果不一致，並證明只有當星系中心距離 $R$ 內分布的質量 $M(R)$ 與 $R$ 成正比時才能解釋觀測結果。

首先，當星系質量 $M$ 集中在中心部時，距離 $R$ 處的軌道速度如下：

\[\frac{GMm}{R^2} = \frac{mv^2}{R}\] \[v = \sqrt{\frac{GM}{R}} \propto \frac{1}{\sqrt{R}}.\]

這種情況下預測軌道速度會如上述兩個圖中的虛線所示以 $1/\sqrt{R}$ 減少，但根據觀測結果，軌道速度 $v$ 與距離 $R$ 無關幾乎保持恆定，所以預測與觀測結果不一致。這種觀測結果只有在 $M(R)\propto R$ 時才能解釋。

用比例常數 $k$ 寫成 $M(R) = kR$，則：

\[v = \sqrt{\frac{GM(R)}{R}} = \sqrt{Gk}\ \text{（常數）}.\]

由此，天體物理學家得出結論：許多星系中必須存在未被發現的「暗物質（dark matter）」，這種暗物質必須佔宇宙質量的 90% 以上。不過暗物質的真面目至今仍未明確揭示，雖然不是主流理論，但也存在修正牛頓動力學（Modified Newtonian Dynamics, MOND）等不假設暗物質存在而試圖解釋觀測結果的嘗試。今天這些研究領域正處於天體物理學的最前沿。