Gravitationsfeld und Gravitationspotential

TL;DR

• Newtons Gravitationsgesetz: $\mathbf{F} = -G\cfrac{mM}{r^2}\mathbf{e}_r$
• Für kontinuierliche Massenverteilungen und Objekte mit Ausdehnung: $\mathbf{F} = -Gm\int_V \cfrac{dM}{r^2}\mathbf{e}_r = -Gm\int_V \cfrac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2} dv^{\prime}$
  • $\rho(\mathbf{r^{\prime}})$: Massendichte am Punkt mit Positionsvektor $\mathbf{r^{\prime}}$ von einem beliebigen Ursprung
  • $dv^{\prime}$: Volumenelement am Punkt mit Positionsvektor $\mathbf{r^{\prime}}$ von einem beliebigen Ursprung
• Gravitationsfeldvektor:
  • Vektor, der die Kraft pro Masseneinheit darstellt, die ein Teilchen in einem von einem Objekt der Masse $M$ erzeugten Feld erfährt
  • $\mathbf{g} = \cfrac{\mathbf{F}}{m} = - G \cfrac{M}{r^2}\mathbf{e}_r = - G \int_V \cfrac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2}dv^\prime$
  • Hat die Dimension von Kraft pro Masseneinheit oder Beschleunigung
• Gravitationspotential:
  • $\mathbf{g} \equiv -\nabla \Phi$
  • Hat die Dimension von (Kraft pro Masseneinheit) $\times$ (Entfernung) oder Energie pro Masseneinheit
  • $\Phi = -G\cfrac{M}{r}$
  • Nur die relative Differenz des Gravitationspotentials ist bedeutsam, nicht der spezifische Wert selbst
  • Üblicherweise wird die Bedingung $\Phi \to 0$ für $r \to \infty$ willkürlich gesetzt, um die Mehrdeutigkeit zu beseitigen
  • $U = m\Phi, \quad \mathbf{F} = -\nabla U$
• Gravitationspotential innerhalb und außerhalb einer Kugelschale (Schalentheorem)
  • Für $R>a$:
    • $\Phi(R>a) = -\cfrac{GM}{R}$
    • Bei der Berechnung des Gravitationspotentials an einem äußeren Punkt aufgrund einer kugelsymmetrischen Massenverteilung kann das entsprechende Objekt als Punktmasse betrachtet werden
  • Für $R<b$:
    • $\Phi(R<b) = -2\pi\rho G(a^2 - b^2)$
    • Innerhalb einer kugelsymmetrischen Massenschale ist das Gravitationspotential unabhängig von der Position konstant, und die wirkende Gravitation ist $0$
  • Für $b<R<a$: $\Phi(b<R<a) = -4\pi\rho G \left( \cfrac{a^2}{2} - \cfrac{b^3}{3R} - \cfrac{R^2}{6} \right)$

Gravitationsfeld

Newtons Gravitationsgesetz

Newton hatte bereits vor 11666 HE das Gravitationsgesetz systematisiert und numerisch verifiziert. Dennoch dauerte es weitere 20 Jahre, bis er 11687 HE seine Ergebnisse in seinem Werk Principia veröffentlichte. Der Grund dafür war, dass er die Berechnungsmethode, bei der Erde und Mond als ausdehnungslose Punktmassen angenommen wurden, nicht rechtfertigen konnte. Glücklicherweise können wir mit der Infinitesimalrechnung, die Newton später selbst erfand, dieses Problem, das für Newton in den 1600er Jahren nicht einfach war, viel leichter beweisen.

Nach Newtons Gravitationsgesetz (Newton’s law of universal gravitation) zieht jedes Massenteilchen alle anderen Teilchen im Universum an, wobei die Kraft proportional zum Produkt der beiden Massen und umgekehrt proportional zum Quadrat ihres Abstands ist. Mathematisch ausgedrückt:

\[\mathbf{F} = -G\frac{mM}{r^2}\mathbf{e}_r \label{eqn:law_of_gravitation}\tag{1}\]

Bildquelle

• Autor: Wikimedia-Benutzer Dennis Nilsson
• Lizenz: CC BY 3.0

Der Einheitsvektor $\mathbf{e}_r$ zeigt von $M$ in Richtung $m$, und das negative Vorzeichen zeigt an, dass die Kraft eine Anziehungskraft ist. Das heißt, $m$ wird zu $M$ hingezogen.

Cavendishs Experiment

Die experimentelle Verifikation dieses Gesetzes und die Bestimmung des $G$-Werts wurde 11798 HE vom britischen Physiker Henry Cavendish durchgeführt. Cavendishs Experiment verwendete eine Torsionswaage, die aus zwei kleinen Kugeln bestand, die an beiden Enden eines leichten Stabs befestigt waren. Diese beiden Kugeln wurden jeweils zu zwei anderen großen Kugeln in ihrer Nähe hingezogen. Der bis heute ermittelte offizielle $G$-Wert beträgt $6.673 \pm 0.010 \times 10^{-11} \mathrm{N\cdot m^2/kg^2}$.

Obwohl $G$ eine der am längsten bekannten Fundamentalkonstanten ist, kennen wir sie mit geringerer Präzision als die meisten anderen Fundamentalkonstanten wie $e$, $c$, $\hbar$. Auch heute noch wird viel geforscht, um den $G$-Wert mit höherer Präzision zu bestimmen.

Fall von Objekten mit Ausdehnung

Das Gesetz in Gleichung ($\ref{eqn:law_of_gravitation}$) kann streng genommen nur auf Punktteilchen angewendet werden. Wenn eine oder beide Seiten Objekte mit einer gewissen Ausdehnung sind, muss zusätzlich angenommen werden, dass das Gravitationsfeld ein lineares Feld ist, um die Kraft zu berechnen. Das heißt, es wird angenommen, dass die gesamte Gravitation, die ein Teilchen der Masse $m$ von mehreren anderen Teilchen erfährt, durch Vektoraddition der einzelnen Kräfte berechnet werden kann. Bei Objekten mit kontinuierlicher Massenverteilung wird die Summe wie folgt durch ein Integral ersetzt:

\[\mathbf{F} = -Gm\int_V \frac{dM}{r^2}\mathbf{e}_r = -Gm\int_V \frac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2} dv^{\prime} \label{eqn:integral_form}\tag{2}\]

• $\rho(\mathbf{r^{\prime}})$: Massendichte am Punkt mit Positionsvektor $\mathbf{r^{\prime}}$ von einem beliebigen Ursprung
• $dv^{\prime}$: Volumenelement am Punkt mit Positionsvektor $\mathbf{r^{\prime}}$ von einem beliebigen Ursprung

Wenn sowohl das Objekt der Masse $M$ als auch das Objekt der Masse $m$ eine Ausdehnung haben, ist zur Berechnung der gesamten Gravitation auch ein zweites Volumenintegral über $m$ erforderlich.

Gravitationsfeldvektor

Der Gravitationsfeldvektor $\mathbf{g}$ wird als Vektor definiert, der die Kraft pro Masseneinheit darstellt, die ein Teilchen in einem von einem Objekt der Masse $M$ erzeugten Feld erfährt:

\[\mathbf{g} = \frac{\mathbf{F}}{m} = - G \frac{M}{r^2}\mathbf{e}_r \label{eqn:g_vector}\tag{3}\]

oder

\[\boxed{\mathbf{g} = - G \int_V \frac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2}dv^\prime} \tag{4}\]

Hier ändert sich die Richtung von $\mathbf{e}_r$ je nach $\mathbf{r^\prime}$.

Diese Größe $\mathbf{g}$ hat die Dimension von Kraft pro Masseneinheit oder Beschleunigung. Der Betrag des Gravitationsfeldvektors $\mathbf{g}$ nahe der Erdoberfläche entspricht der Größe, die wir Gravitationsbeschleunigungskonstante nennen, mit $|\mathbf{g}| \approx 9.80\mathrm{m/s^2}$.

Gravitationspotential

Definition

Der Gravitationsfeldvektor $\mathbf{g}$ ändert sich mit $1/r^2$ und erfüllt daher die Bedingung ($\nabla \times \mathbf{g} \equiv 0$) für die Darstellung als Gradient einer Skalarfunktion (Potential). Daher kann geschrieben werden:

\[\mathbf{g} \equiv -\nabla \Phi \label{eqn:gradient_phi}\tag{5}\]

Hier wird $\Phi$ als Gravitationspotential bezeichnet und hat die Dimension von (Kraft pro Masseneinheit) $\times$ (Entfernung) oder Energie pro Masseneinheit.

Da $\mathbf{g}$ nur vom Radius abhängt, ändert sich auch $\Phi$ nur mit $r$. Aus den Gleichungen ($\ref{eqn:g_vector}$) und ($\ref{eqn:gradient_phi}$) folgt:

\[\nabla\Phi = \frac{d\Phi}{dr}\mathbf{e}_r = G\frac{M}{r^2}\mathbf{e}_r\]

Integration ergibt:

\[\boxed{\Phi = -G\frac{M}{r}} \label{eqn:g_potential}\tag{6}\]

Da nur die relative Differenz des Gravitationspotentials bedeutsam ist und nicht der spezifische Wert selbst, kann die Integrationskonstante weggelassen werden. Üblicherweise wird die Bedingung $\Phi \to 0$ für $r \to \infty$ willkürlich gesetzt, um die Mehrdeutigkeit zu beseitigen, und Gleichung ($\ref{eqn:g_potential}$) erfüllt auch diese Bedingung.

Das Gravitationspotential bei kontinuierlicher Massenverteilung ist:

\[\Phi = -G\int_V \frac{\rho(\mathbf{r\prime})}{r}dv^\prime \label{eqn:g_potential_v}\tag{7}\]

Bei Oberflächenverteilung der Masse in einer dünnen Schale:

\[\Phi = -G\int_S \frac{\rho_s}{r}da^\prime. \label{eqn:g_potential_s}\tag{8}\]

Und für eine lineare Massenquelle mit Liniendichte $\rho_l$:

\[\Phi = -G\int_\Gamma \frac{\rho_l}{r}ds^\prime. \label{eqn:g_potential_l}\tag{9}\]

Physikalische Bedeutung

Betrachten wir die Arbeit pro Masseneinheit $dW^\prime$, die ein Objekt verrichtet, wenn es sich um $d\mathbf{r}$ in einem Gravitationsfeld bewegt.

\[\begin{align*} dW^\prime &= -\mathbf{g}\cdot d\mathbf{r} = (\nabla \Phi)\cdot d\mathbf{r} \\ &= \sum_i \frac{\partial \Phi}{\partial x_i}dx_i = d\Phi \label{eqn:work}\tag{10} \end{align*}\]

In dieser Gleichung ist $\Phi$ nur eine Funktion der Ortskoordinaten, dargestellt als $\Phi=\Phi(x_1, x_2, x_3) = \Phi(x_i)$. Daher ist die Arbeit pro Masseneinheit, die ein Objekt verrichtet, wenn es von einem Punkt zu einem anderen in einem Gravitationsfeld bewegt wird, gleich der Potentialdifferenz zwischen diesen beiden Punkten.

Wenn das Gravitationspotential an unendlich entfernten Orten als $0$ definiert wird, kann $\Phi$ an einem beliebigen Punkt als die Arbeit pro Masseneinheit interpretiert werden, die erforderlich ist, um das Objekt von unendlich entfernten Orten zu diesem Punkt zu bewegen. Da die potentielle Energie eines Objekts gleich dem Produkt seiner Masse und des Gravitationspotentials $\Phi$ ist, gilt für die potentielle Energie $U$:

\[U = m\Phi. \label{eqn:potential_e}\tag{11}\]

Daher wird die Gravitation, die auf ein Objekt wirkt, durch Hinzufügen eines negativen Vorzeichens zum Gradienten der potentiellen Energie des Objekts erhalten:

\[\mathbf{F} = -\nabla U \label{eqn:force_and_potential}\tag{12}\]

Wenn sich ein Objekt in einem von einer Masse erzeugten Gravitationsfeld befindet, entsteht immer eine potentielle Energie. Diese potentielle Energie befindet sich streng genommen im Feld selbst, wird aber konventionell als potentielle Energie des Objekts bezeichnet.

Beispiel: Gravitationspotential innerhalb und außerhalb einer Kugelschale (Schalentheorem)

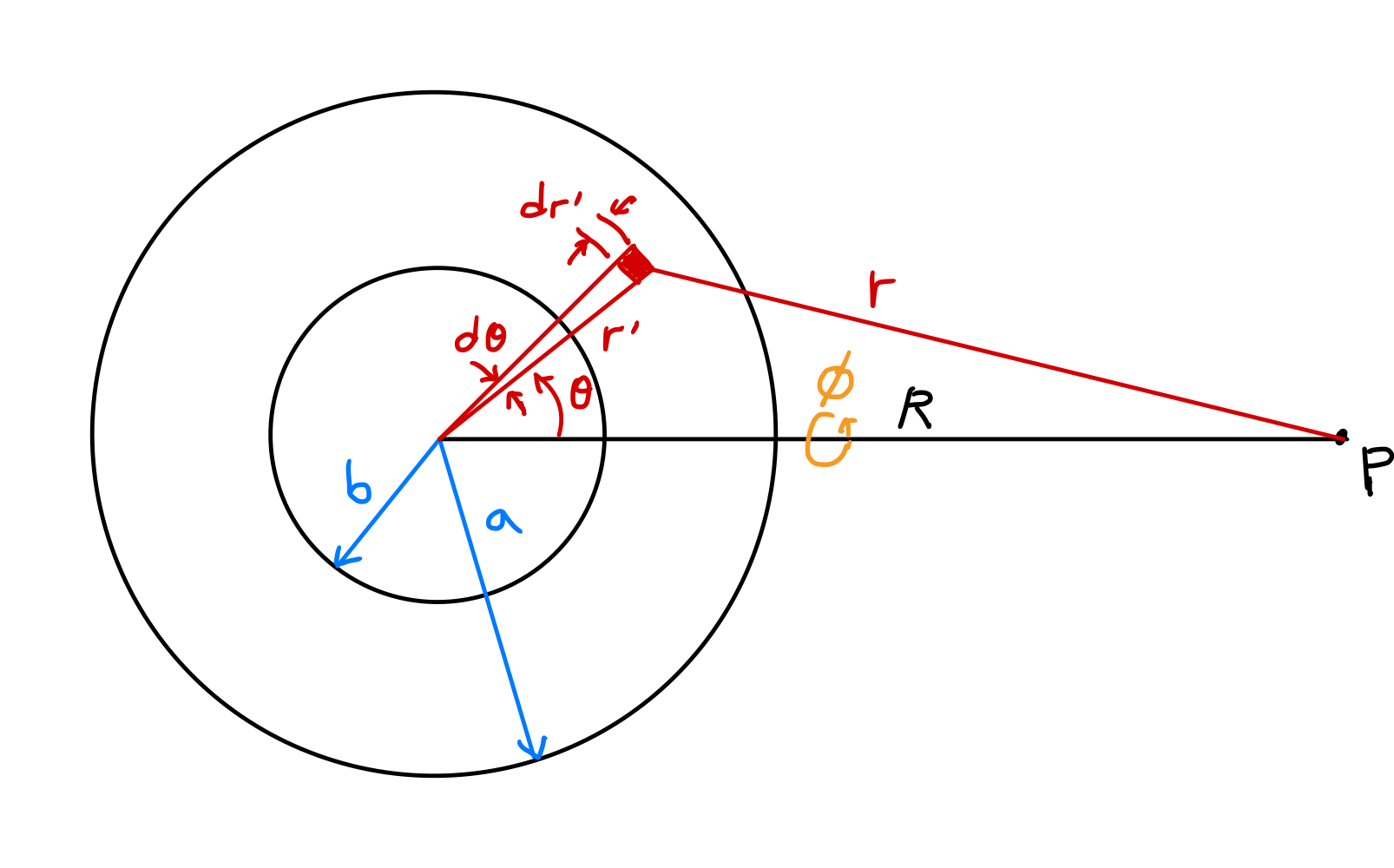
Koordinatensystem & Darstellung des Gravitationspotentials als Integral

Berechnen wir das Gravitationspotential innerhalb und außerhalb einer gleichmäßigen Kugelschale mit innerem Radius $b$ und äußerem Radius $a$. Die Gravitation durch eine Kugelschale kann auch durch direkte Berechnung der Kraftkomponenten, die auf eine Masseneinheit im Feld wirken, erhalten werden, aber die Potentialmethode ist einfacher.

Berechnen wir das Potential am Punkt $P$ in der Entfernung $R$ vom Zentrum in der obigen Abbildung. Bei gleichmäßiger Massenverteilung der Schale ist $\rho(r^\prime)=\rho$, und aufgrund der Symmetrie bezüglich des Azimuthwinkels $\phi$ um die Linie, die das Zentrum der Kugel mit Punkt $P$ verbindet:

\[\begin{align*} \Phi &= -G\int_V \frac{\rho(r^\prime)}{r}dv^\prime \\ &= -\rho G \int_0^{2\pi} \int_0^\pi \int_b^a \frac{1}{r}(dr^\prime)(r^\prime d\theta)(r^\prime \sin\theta\, d\phi) \\ &= -\rho G \int_0^{2\pi} d\phi \int_b^a {r^\prime}^2 dr^\prime \int_0^\pi \frac{\sin\theta}{r}d\theta \\ &= -2\pi\rho G \int_b^a {r^\prime}^2 dr^\prime \int_0^\pi \frac{\sin\theta}{r}d\theta. \label{eqn:spherical_shell_1}\tag{13} \end{align*}\]

Nach dem Kosinussatz:

\[r^2 = {r^\prime}^2 + R^2 - 2r^\prime R \cos\theta \label{eqn:law_of_cosines}\tag{14}\]

Da $R$ konstant ist, ergibt die Differentiation dieser Gleichung nach $r^\prime$:

\[2rdr = 2r^\prime R \sin\theta d\theta\] \[\frac{\sin\theta}{r}d\theta = \frac{dr}{r^\prime R} \tag{15}\]

Einsetzen in Gleichung ($\ref{eqn:spherical_shell_1}$):

\[\Phi = -\frac{2\pi\rho G}{R} \int_b^a r^\prime dr^\prime \int_{r_\mathrm{min}}^{r_\mathrm{max}} dr. \label{eqn:spherical_shell_2}\tag{16}\]

Hier werden $r_\mathrm{max}$ und $r_\mathrm{min}$ durch die Position des Punktes $P$ bestimmt.

Für $R>a$

\(\begin{align*} \Phi(R>a) &= -\frac{2\pi\rho G}{R} \int_b^a r^\prime dr^\prime \int_{R-r^\prime}^{R+r^\prime} dr \\ &= - \frac{4\pi\rho G}{R} \int_b^a {r^\prime}^2 dr^\prime \\ &= - \frac{4}{3}\frac{\pi\rho G}{R}(a^3 - b^3). \label{eqn:spherical_shell_outside_1}\tag{17} \end{align*}\)

Die Masse $M$ der Kugelschale ist:

\[M = \frac{4}{3}\pi\rho(a^3 - b^3) \label{eqn:mass_of_shell}\tag{18}\]

Daher ist das Potential:

\[\boxed{\Phi(R>a) = -\frac{GM}{R}} \label{eqn:spherical_shell_outside_2}\tag{19}\]

Vergleicht man das Gravitationspotential einer Punktmasse der Masse $M$ aus Gleichung ($\ref{eqn:g_potential}$) mit dem gerade erhaltenen Ergebnis ($\ref{eqn:spherical_shell_outside_2}$), stellt man fest, dass sie identisch sind. Dies bedeutet, dass bei der Berechnung des Gravitationspotentials an einem äußeren Punkt aufgrund einer kugelsymmetrischen Massenverteilung davon ausgegangen werden kann, dass die gesamte Masse im Zentrum konzentriert ist. Die meisten kugelförmigen Himmelskörper einer bestimmten Größe wie Erde oder Mond fallen in diese Kategorie, da sie wie Matroschka-Puppen als unendlich viele Kugelschalen mit demselben Zentrum aber unterschiedlichen Durchmessern betrachtet werden können. Dies ist die Grundlage für die Gültigkeit der Annahme, Himmelskörper wie Erde oder Mond als ausdehnungslose Punktmassen zu betrachten, die am Anfang dieses Artikels erwähnt wurde.

Für $R<b$

\(\begin{align*} \Phi(R<b) &= -\frac{2\pi\rho G}{R} \int_b^a r^\prime dr^\prime \int_{r^\prime - R}^{r^\prime + R}dr \\ &= -4\pi\rho G \int_b^a r^\prime dr^\prime \\ &= -2\pi\rho G(a^2 - b^2). \label{eqn:spherical_shell_inside}\tag{20} \end{align*}\)

Innerhalb einer kugelsymmetrischen Massenschale ist das Gravitationspotential unabhängig von der Position konstant, und die wirkende Gravitation ist $0$.

Dies ist auch ein Hauptgrund dafür, dass die “Hohlerde-Theorie”, eine der typischen Pseudowissenschaften, Unsinn ist. Wenn die Erde, wie die Hohlerde-Theorie behauptet, die Form einer Kugelschale hätte und innen hohl wäre, würde die Erdgravitation auf alle Objekte innerhalb dieser Höhlung nicht wirken. Angesichts der Masse und des Volumens der Erde kann es keine Erdhöhlung geben, und selbst wenn es eine gäbe, würden die Lebewesen dort nicht mit der Innenseite der Kugelschale als Boden leben, sondern wie in einer Raumstation in einem schwerelosen Zustand schweben.
Mikroorganismen können durchaus einige Kilometer tief in unterirdischen Schichten leben, aber zumindest nicht in der Form, wie die Hohlerde-Theorie behauptet. Ich mag Jules Vernes Roman “Reise zum Mittelpunkt der Erde” und den Film “Die Reise zum Mittelpunkt der Erde” sehr, aber fiktive Werke sollten als Fiktion genossen werden, nicht ernsthaft geglaubt.

Für $b<R<a$

\(\begin{align*} \Phi(b<R<a) &= -\frac{4\pi\rho G}{3R}(R^3 - b^3) - 2\pi\rho G(a^2 - R^2) \\ &= -4\pi\rho G \left( \frac{a^2}{2} - \frac{b^3}{3R} - \frac{R^2}{6} \right) \label{eqn:within_spherical_shell}\tag{21} \end{align*}\)

Ergebnisse

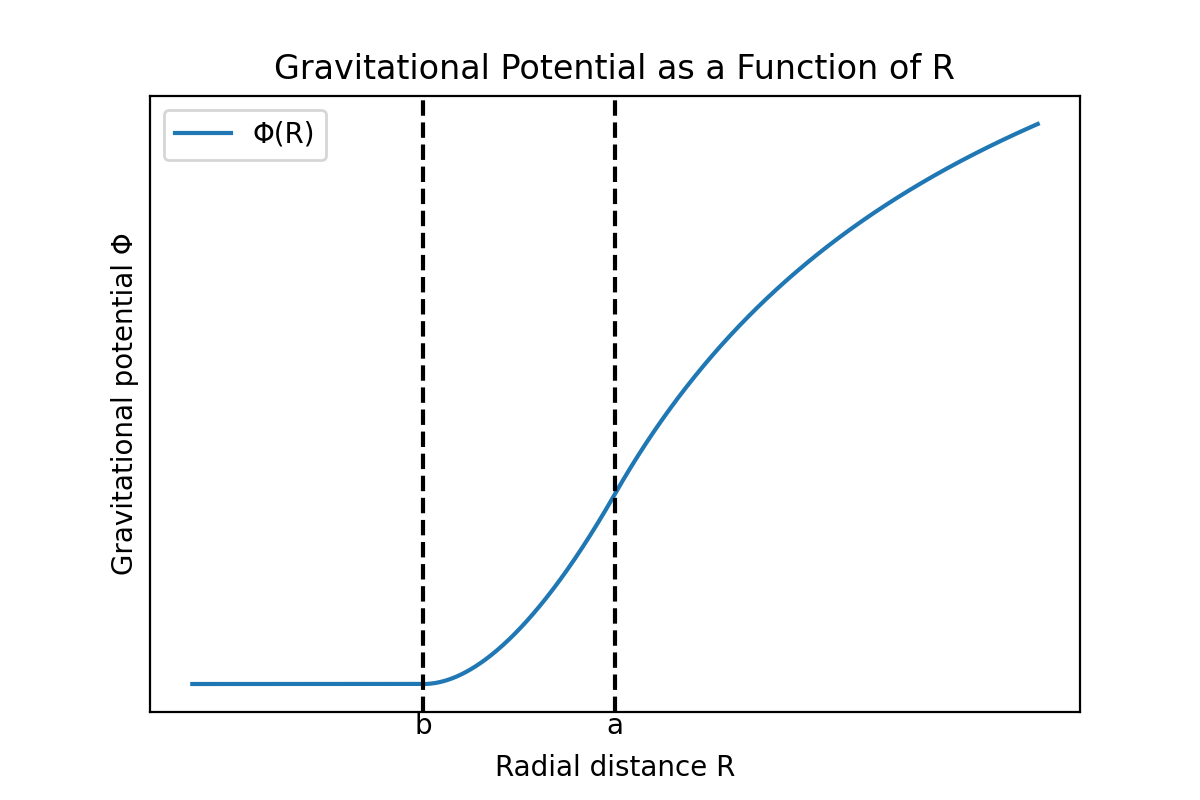
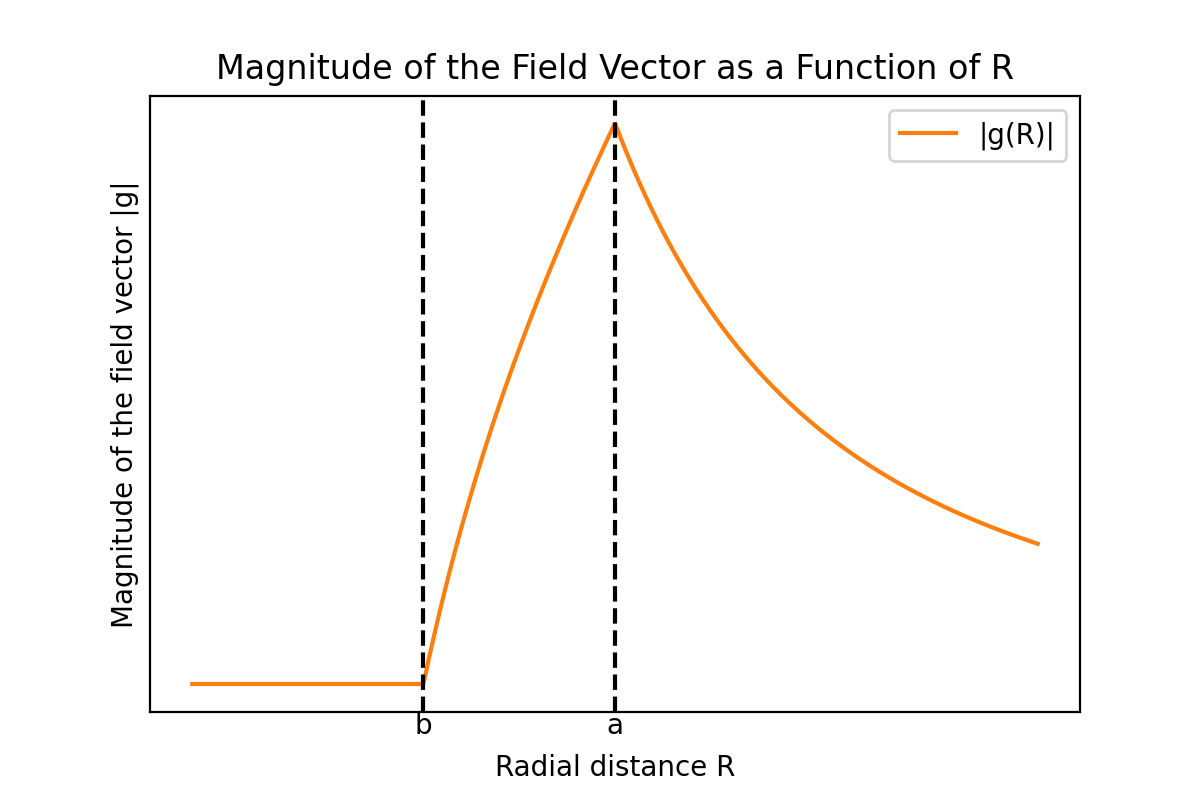
Die zuvor berechneten Gravitationspotentiale $\Phi$ in den drei Bereichen und die entsprechenden Beträge der Gravitationsfeldvektoren $|\mathbf{g}|$ als Funktion der Entfernung $R$ sind grafisch wie folgt dargestellt:

• Python-Visualisierungscode: yunseo-kim/physics-visualizations Repository
• Lizenz: Siehe hier

Man kann sehen, dass das Gravitationspotential und der Betrag des Gravitationsfeldvektors stetig sind. Wenn das Gravitationspotential an einem Punkt unstetig wäre, würde der Gradient des Potentials, also die Gravitationsstärke, an diesem Punkt unendlich werden, was physikalisch nicht sinnvoll ist. Daher muss die Potentialfunktion an allen Punkten stetig sein. Die Ableitung des Gravitationsfeldvektors ist jedoch an der Innen- und Außenseite der Schale unstetig.

Beispiel: Galaktische Rotationskurve

Astronomischen Beobachtungen zufolge ist die meiste beobachtbare Masse in vielen rotierenden Spiralgalaxien wie der Milchstraße oder der Andromeda-Galaxie hauptsächlich in der Nähe des Zentrums konzentriert. Die Orbitalgeschwindigkeiten der Massen in solchen Spiralgalaxien stimmen jedoch, wie im folgenden Diagramm zu sehen ist, stark mit den theoretisch aus der beobachtbaren Massenverteilung vorhergesagten Werten nicht überein und sind ab einer bestimmten Entfernung nahezu konstant.

Bildquelle

• Autor: Wikipedia-Benutzer PhilHibbs
• Lizenz: Public Domain

Rotationskurve der Spiralgalaxie M33 (Dreiecksgalaxie)

• Autor: Wikimedia-Benutzer Mario De Leo
• Lizenz: CC BY-SA 4.0

Lassen Sie uns die Orbitalgeschwindigkeit in Abhängigkeit von der Entfernung vorhersagen, wenn die Masse der Galaxie im Zentrum konzentriert ist, bestätigen, dass diese Vorhersage nicht mit den Beobachtungsergebnissen übereinstimmt, und zeigen, dass die Masse $M(R)$, die innerhalb der Entfernung $R$ vom galaktischen Zentrum verteilt ist, proportional zu $R$ sein muss, um die Beobachtungsergebnisse zu erklären.

Zunächst berechnen wir die Orbitalgeschwindigkeit in der Entfernung $R$, wenn die galaktische Masse $M$ im Zentrum konzentriert ist:

\[\frac{GMm}{R^2} = \frac{mv^2}{R}\] \[v = \sqrt{\frac{GM}{R}} \propto \frac{1}{\sqrt{R}}.\]

In diesem Fall wird eine Orbitalgeschwindigkeit vorhergesagt, die wie die gestrichelten Linien in den beiden obigen Diagrammen mit $1/\sqrt{R}$ abnimmt. Den Beobachtungsergebnissen zufolge ist die Orbitalgeschwindigkeit $v$ jedoch nahezu konstant, unabhängig von der Entfernung $R$, sodass Vorhersage und Beobachtung nicht übereinstimmen. Diese Beobachtungsergebnisse können nur erklärt werden, wenn $M(R)\propto R$ gilt.

Setzt man mit der Proportionalitätskonstante $k$ $M(R) = kR$, so ergibt sich:

\[v = \sqrt{\frac{GM(R)}{R}} = \sqrt{Gk}\ \text{(konstant)}.\]

Daraus schließen Astrophysiker, dass es in vielen Galaxien unentdeckte “Dunkle Materie” geben muss und diese Dunkle Materie mehr als 90% der Masse des Universums ausmachen muss. Die Identität der Dunklen Materie ist jedoch noch nicht eindeutig geklärt, und obwohl es nicht die Haupttheorie ist, gibt es auch Versuche wie die Modifizierte Newtonsche Dynamik (Modified Newtonian Dynamics, MOND), die die Beobachtungsergebnisse ohne die Annahme der Existenz Dunkler Materie zu erklären versuchen. Heute stehen solche Forschungsgebiete an der Spitze der Astrophysik.