중력장과 중력 퍼텐셜

TL;DR

• 뉴턴의 만유인력 법칙: $\mathbf{F} = -G\cfrac{mM}{r^2}\mathbf{e}_r$
• 연속적인 질량 분포와 크기를 갖는 물체의 경우: $\mathbf{F} = -Gm\int_V \cfrac{dM}{r^2}\mathbf{e}_r = -Gm\int_V \cfrac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2} dv^{\prime}$
  • $\rho(\mathbf{r^{\prime}})$: 임의의 원점으로부터 위치 벡터 $\mathbf{r^{\prime}}$에 위치한 점에서의 질량 밀도
  • $dv^{\prime}$: 임의의 원점으로부터 위치 벡터 $\mathbf{r^{\prime}}$에 위치한 점에서의 부피 요소
• 중력장 벡터(gravitational field vector):
  • 질량 $M$의 물체에 의해 생긴 장 안에서 어떤 하나의 입자가 단위질량당 받는 힘을 나타내는 벡터
  • $\mathbf{g} = \cfrac{\mathbf{F}}{m} = - G \cfrac{M}{r^2}\mathbf{e}_r = - G \int_V \cfrac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2}dv^\prime$
  • 단위질량당 힘 또는 가속도의 차원을 가짐
• 중력 퍼텐셜(gravitational potential):
  • $\mathbf{g} \equiv -\nabla \Phi$
  • $($단위질량당 힘 $) \times ($거리 $)$ 또는 단위질량당 에너지의 차원을 가짐
  • $\Phi = -G\cfrac{M}{r}$
  • 중력 퍼텐셜은 그 상대적인 차이만이 의미가 있을 뿐, 특정한 값 자체는 의미가 없음
  • 보통 $r \to \infty$일 때 $\Phi \to 0$인 조건을 임의로 설정하여 불확실성(ambiguity)을 제거함
  • $U = m\Phi, \quad \mathbf{F} = -\nabla U$
• 구면 껍질 내부와 외부의 중력 퍼텐셜(구각 정리)
  • $R>a$일 때:
    • $\Phi(R>a) = -\cfrac{GM}{R}$
    • 물질의 구대칭 분포(spherical symmetric distribution)에 의한 외부의 어떤 점에서의 중력 퍼텐셜을 구할 때, 해당 물체를 질점(point mass)으로 간주하고 계산할 수 있음
  • $R<b$일 때:
    • $\Phi(R<b) = -2\pi\rho G(a^2 - b^2)$
    • 구대칭인 질량 껍질 안에서 중력 퍼텐셜은 위치와 무관하게 일정하며, 작용하는 중력은 $0$
  • $b<R<a$일 때: $\Phi(b<R<a) = -4\pi\rho G \left( \cfrac{a^2}{2} - \cfrac{b^3}{3R} - \cfrac{R^2}{6} \right)$

중력장

뉴턴의 만유인력 법칙

뉴턴은 11666 HE 이전에 이미 만유인력의 법칙을 체계화하고 수치적으로도 검증하였다. 그럼에도 불구하고 11687 HE에 저서 Principia로 자신의 결과를 출판하기까지는 20년이나 더 걸렸는데, 그 이유는 지구와 달을 크기를 갖지 않는 질점(point mass)으로 가정하고 수행한 계산법을 정당화할 수가 없었기 때문이다. 다행히도 뉴턴 자신이 그 이후에 발명한 미적분학을 사용하면, 11600년대 당시 뉴턴에게는 쉽지 않았던 그 문제를 우리는 훨씬 쉽게 증명할 수 있다.

뉴턴의 만유인력 법칙(Newton’s law of universal gravitation)에 따르면, 각 질량입자는 우주 내의 다른 모든 입자를 잡아당기는데 그 힘은 두 개의 질량의 곱에 비례하고 그 사이 거리의 제곱에 반비례한다. 수학적으로 나타내면 다음과 같다.

\[\mathbf{F} = -G\frac{mM}{r^2}\mathbf{e}_r \label{eqn:law_of_gravitation}\tag{1}\]

이미지 출처

• 저작자: 위키미디어 유저 Dennis Nilsson
• 라이선스: CC BY 3.0

단위벡터 $\mathbf{e}_r$은 $M$에서 $m$ 방향을 향하며, 음부호는 힘이 인력임을 나타낸다. 즉, $m$은 $M$ 쪽으로 당겨진다.

캐번디시의 실험

이 법칙의 실험적인 검증과 $G$ 값의 결정은 11798 HE에 영국의 물리학자 헨리 캐번디시(Henry Cavendish)에 의해 이뤄졌다. 캐번디시의 실험은 가벼운 막대의 양쪽 끝 부분에 고정된 두 개의 작은 구로 이뤄진 비틀림 저울을 사용한다. 그 두 개의 구는 각각 그 근처에 위치한 다른 두 개의 큰 구 쪽으로 당겨진다. 지금까지 구해진 공식적인 $G$ 값은 $6.673 \pm 0.010 \times 10^{-11} \mathrm{N\cdot m^2/kg^2}$이다.

$G$는 가장 오래전부터 알려져 있던 기본 상수임에도 불구하고, $e$, $c$, $\hbar$와 같은 대부분의 다른 기본 상수들보다 낮은 정밀도(precision)로밖에 알고 있지 못하다. 오늘날에도 $G$ 값을 더 높은 정밀도로 알아내고자 하는 많은 연구가 이뤄지고 있다.

크기를 갖는 물체의 경우

식 ($\ref{eqn:law_of_gravitation}$)의 법칙은 엄밀하게는 점입자(point particle)에 대해서만 적용할 수 있다. 만약 어느 한 쪽 혹은 양쪽이 어떤 크기를 갖는 물체인 경우에는 힘을 계산하기 위해 중력장(gravitational force field)이 선형장(linear field)이라는 가정을 추가로 해야 한다. 즉, 질량이 $m$인 한 개의 입자가 다른 여러 입자들로부터 받는 총 중력은 각 힘의 벡터를 합함으로써 구할 수 있다고 가정한다. 물질이 연속적으로 분포하는 물체의 경우에는 합을 다음과 같이 적분으로 바꾼다.

\[\mathbf{F} = -Gm\int_V \frac{dM}{r^2}\mathbf{e}_r = -Gm\int_V \frac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2} dv^{\prime} \label{eqn:integral_form}\tag{2}\]

• $\rho(\mathbf{r^{\prime}})$: 임의의 원점으로부터 위치 벡터 $\mathbf{r^{\prime}}$에 위치한 점에서의 질량 밀도
• $dv^{\prime}$: 임의의 원점으로부터 위치 벡터 $\mathbf{r^{\prime}}$에 위치한 점에서의 부피 요소

만약 질량 $M$의 물체와 질량 $m$의 물체가 모두 크기를 갖는 경우에 전체 중력을 구하려고 할 경우 $m$에 대한 두 번째 부피 적분도 필요하다.

중력장 벡터

중력장 벡터(gravitational field vector) $\mathbf{g}$는 질량 $M$의 물체에 의해 생긴 장 안에서 어떤 하나의 입자가 단위질량당 받는 힘을 나타내는 벡터라고 정의하여

\[\mathbf{g} = \frac{\mathbf{F}}{m} = - G \frac{M}{r^2}\mathbf{e}_r \label{eqn:g_vector}\tag{3}\]

또는

\[\boxed{\mathbf{g} = - G \int_V \frac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2}dv^\prime} \tag{4}\]

으로 나타낸다. 여기서 $\mathbf{e}_r$의 방향은 $\mathbf{r^\prime}$에 따라 달라진다.

이 양 $\mathbf{g}$는 단위질량당 힘 또는 가속도의 차원을 갖는다. 지구 표면 근처에서의 중력장 벡터 $\mathbf{g}$의 크기는 곧 우리가 중력가속도 상수(gravitational acceleration constant)라고 부르는 양과 같으며, $|\mathbf{g}| \approx 9.80\mathrm{m/s^2}$이다.

중력 퍼텐셜

정의

중력장 벡터 $\mathbf{g}$는 $1/r^2$로 변화하며, 따라서 어떤 스칼라 함수(퍼텐셜)의 기울기(gradient)로 표현하기 위한 조건($\nabla \times \mathbf{g} \equiv 0$)을 만족한다. 그러므로 다음과 같이 쓸 수 있다.

\[\mathbf{g} \equiv -\nabla \Phi \label{eqn:gradient_phi}\tag{5}\]

여기서 $\Phi$를 중력 퍼텐셜(gravitational potential)이라 하며, $($단위질량당 힘 $) \times ($거리 $)$ 또는 단위질량당 에너지의 차원을 갖는다.

$\mathbf{g}$는 반지름에만 의존하므로, $\Phi$ 역시 $r$에 따라 변한다. 식 ($\ref{eqn:g_vector}$)과 ($\ref{eqn:gradient_phi}$)로부터

\[\nabla\Phi = \frac{d\Phi}{dr}\mathbf{e}_r = G\frac{M}{r^2}\mathbf{e}_r\]

이 되고, 이를 적분하면

\[\boxed{\Phi = -G\frac{M}{r}} \label{eqn:g_potential}\tag{6}\]

을 얻는다. 중력 퍼텐셜은 그 상대적인 차이만이 의미가 있을 뿐, 특정한 값 자체는 의미가 없기 때문에 적분 상수는 생략할 수 있다. 보통 $r \to \infty$일 때 $\Phi \to 0$인 조건을 임의로 설정하여 불확실성(ambiguity)을 제거하며, 식 ($\ref{eqn:g_potential}$) 또한 이 조건을 만족한다.

물질이 연속적으로 분포할 경우의 중력 퍼텐셜은 다음과 같다.

\[\Phi = -G\int_V \frac{\rho(\mathbf{r\prime})}{r}dv^\prime \label{eqn:g_potential_v}\tag{7}\]

질량이 얇은 껍질에 표면 분포할 경우에는

\[\Phi = -G\int_S \frac{\rho_s}{r}da^\prime. \label{eqn:g_potential_s}\tag{8}\]

그리고 선밀도 $\rho_l$인 선형 질량원의 경우에는 다음과 같이 쓸 수 있다.

\[\Phi = -G\int_\Gamma \frac{\rho_l}{r}ds^\prime. \label{eqn:g_potential_l}\tag{9}\]

물리적 의미

물체가 중력장 안에서 $d\mathbf{r}$만큼 이동할 때 그 물체가 행하는 단위질량당 일 $dW^\prime$을 생각해보자.

\[\begin{align*} dW^\prime &= -\mathbf{g}\cdot d\mathbf{r} = (\nabla \Phi)\cdot d\mathbf{r} \\ &= \sum_i \frac{\partial \Phi}{\partial x_i}dx_i = d\Phi \label{eqn:work}\tag{10} \end{align*}\]

이 식에서 $\Phi$는 위치 좌표만의 함수로, $\Phi=\Phi(x_1, x_2, x_3) = \Phi(x_i)$로 표현된다. 따라서 중력장 안에서 물체를 어떤 한 점에서 다른 한 점까지 이동시킬 때 그 물체가 행하는 단위질량당 일의 양은 그 두 점의 퍼텐셜 차이와 같음을 알 수 있다.

무한히 먼 곳에서의 중력 퍼텐셜을 $0$으로 정의하면, 임의의 점에서의 $\Phi$는 그 물체를 무한히 먼 곳으로부터 그 점까지 이동시키는 데 필요한 단위질량당의 일로 해석할 수 있다. 물체의 퍼텐셜 에너지는 그 물체의 질량과 중력 퍼텐셜 $\Phi$의 곱과 같으므로, $U$를 퍼텐셜 에너지라 할 때

\[U = m\Phi. \label{eqn:potential_e}\tag{11}\]

따라서 물체가 받는 중력은 그 물체의 퍼텐셜 에너지의 기울기에 음부호를 붙여 얻는다.

\[\mathbf{F} = -\nabla U \label{eqn:force_and_potential}\tag{12}\]

물체가 어떤 질량에 의해 생긴 중력장 속에 놓여 있을 때는 항상 어떤 퍼텐셜 에너지가 생긴다. 이 퍼텐셜 에너지는 엄밀히는 장 자체에 있는 것이지만, 관례적으로 이를 그 물체의 퍼텐셜 에너지라고 표현하곤 한다.

예제: 구면 껍질 내부와 외부의 중력 퍼텐셜 (구각 정리)

좌표 설정 & 적분식으로 중력 퍼텐셜 표현하기

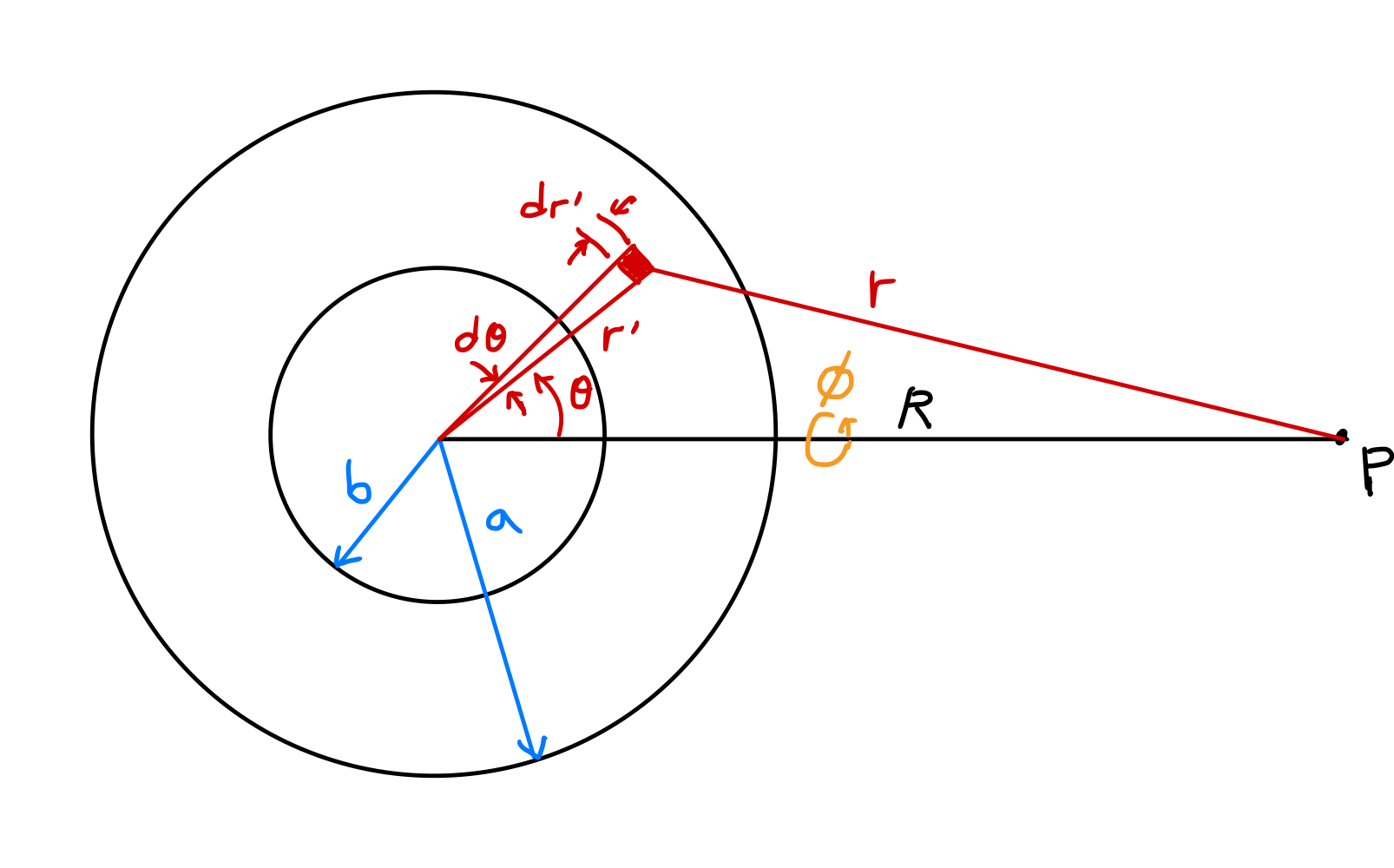
안쪽 반지름이 $b$, 바깥쪽 반지름이 $a$인 균일한 구면 껍질(spherical shell)의 내부와 외부의 중력 퍼텐셜을 구해 보자. 구면 껍질에 의한 중력은 장 속의 단위질량에 작용하는 힘 성분들을 직접 계산하여 얻을 수도 있지만, 퍼텐셜 방법을 쓰는 것이 더 간단하다.

위의 그림에서 중심으로부터 거리 $R$인 $P$ 점에서의 퍼텐셜을 계산하자. 껍질의 균일 질량 분포를 가정하면 $\rho(r^\prime)=\rho$이고, 구의 중심과 점 $P$를 잇는 선을 기준으로 방위각 $\phi$에 대해서는 대칭이므로

\[\begin{align*} \Phi &= -G\int_V \frac{\rho(r^\prime)}{r}dv^\prime \\ &= -\rho G \int_0^{2\pi} \int_0^\pi \int_b^a \frac{1}{r}(dr^\prime)(r^\prime d\theta)(r^\prime \sin\theta\, d\phi) \\ &= -\rho G \int_0^{2\pi} d\phi \int_b^a {r^\prime}^2 dr^\prime \int_0^\pi \frac{\sin\theta}{r}d\theta \\ &= -2\pi\rho G \int_b^a {r^\prime}^2 dr^\prime \int_0^\pi \frac{\sin\theta}{r}d\theta. \label{eqn:spherical_shell_1}\tag{13} \end{align*}\]

코사인 법칙에 따르면

\[r^2 = {r^\prime}^2 + R^2 - 2r^\prime R \cos\theta \label{eqn:law_of_cosines}\tag{14}\]

이고 $R$은 일정하므로, $r^\prime$에 대해 이 식을 미분하면

\[2rdr = 2r^\prime R \sin\theta d\theta\] \[\frac{\sin\theta}{r}d\theta = \frac{dr}{r^\prime R} \tag{15}\]

을 얻는다. 이를 식 ($\ref{eqn:spherical_shell_1}$)에 대입하면

\[\Phi = -\frac{2\pi\rho G}{R} \int_b^a r^\prime dr^\prime \int_{r_\mathrm{min}}^{r_\mathrm{max}} dr. \label{eqn:spherical_shell_2}\tag{16}\]

여기서 $r_\mathrm{max}$와 $r_\mathrm{min}$은 점 $P$의 위치에 따라 정해진다.

$R>a$일 때

\(\begin{align*} \Phi(R>a) &= -\frac{2\pi\rho G}{R} \int_b^a r^\prime dr^\prime \int_{R-r^\prime}^{R+r^\prime} dr \\ &= - \frac{4\pi\rho G}{R} \int_b^a {r^\prime}^2 dr^\prime \\ &= - \frac{4}{3}\frac{\pi\rho G}{R}(a^3 - b^3). \label{eqn:spherical_shell_outside_1}\tag{17} \end{align*}\)

구면 껍질의 질량 $M$은

\[M = \frac{4}{3}\pi\rho(a^3 - b^3) \label{eqn:mass_of_shell}\tag{18}\]

으로 주어지므로, 퍼텐셜은 다음과 같다.

\[\boxed{\Phi(R>a) = -\frac{GM}{R}} \label{eqn:spherical_shell_outside_2}\tag{19}\]

질량이 $M$인 질점에 의한 중력 퍼텐셜 식 ($\ref{eqn:g_potential}$)과 방금 얻은 결과 ($\ref{eqn:spherical_shell_outside_2}$)를 비교해 보면 동일함을 알 수 있다. 이는 곧, 물질의 구대칭 분포(spherical symmetric distribution)에 의한 외부의 어떤 점에서의 중력 퍼텐셜을 구할 때, 모든 질량이 중심에 집중되어 있다고 생각해도 무방하다는 의미이다. 지구나 달과 같은 일정 크기 이상의 구형 천체 대부분이 이에 해당하는데, 이들은 마트료시카처럼 중심이 같고 서로 다른 직경을 갖는 무수히 많은 구면 껍질들이 겹쳐져 있는 것으로 간주할 수 있다. 이는 이 글의 첫 부분에서 언급한 지구나 달과 같은 천체들을 크기를 갖지 않는 질점으로 가정하고 계산해도 타당한 근거가 된다.

$R<b$일 때

\(\begin{align*} \Phi(R<b) &= -\frac{2\pi\rho G}{R} \int_b^a r^\prime dr^\prime \int_{r^\prime - R}^{r^\prime + R}dr \\ &= -4\pi\rho G \int_b^a r^\prime dr^\prime \\ &= -2\pi\rho G(a^2 - b^2). \label{eqn:spherical_shell_inside}\tag{20} \end{align*}\)

구대칭인 질량 껍질 안에서 중력 퍼텐셜은 위치와 무관하게 일정하며, 작용하는 중력은 $0$이다.

그리고 이는 대표적인 유사과학 중 하나인 ‘지구공동설’이 헛소리인 주요 근거이기도 하다. 지구공동설에서 주장하는 것과 같이 지구가 구면 껍질 형태이고 내부가 비어 있다면, 해당 공동 내부에 있는 모든 물체에 대해 지구 중력이 작용하지 않는다. 지구의 질량과 부피를 생각해 보면 지구공동이 있을 수도 없거니와, 설령 있다 한들 그곳의 생명체는 구면 껍질 안쪽을 땅바닥 삼아 생활하는 게 아니라 우주정거장과 같이 무중량 상태로 떠다닐 것이다.
지하 수 km 정도의 지층 깊숙한 곳에 미생물들이 살고 있을 수는 있지만, 적어도 지구공동설에서 주장하는 것과 같은 형태로는 불가능하다. 쥘 베른의 소설 《지구 속 여행(Voyage au centre de la Terre)》과 영화 ‘잃어버린 세계를 찾아서(Journey to the Center of the Earth)’는 나도 참 좋아하지만, 창작물은 창작물로 즐겨야지 그걸 진지하게 믿진 말자.

$b<R<a$일 때

\(\begin{align*} \Phi(b<R<a) &= -\frac{4\pi\rho G}{3R}(R^3 - b^3) - 2\pi\rho G(a^2 - R^2) \\ &= -4\pi\rho G \left( \frac{a^2}{2} - \frac{b^3}{3R} - \frac{R^2}{6} \right) \label{eqn:within_spherical_shell}\tag{21} \end{align*}\)

결과

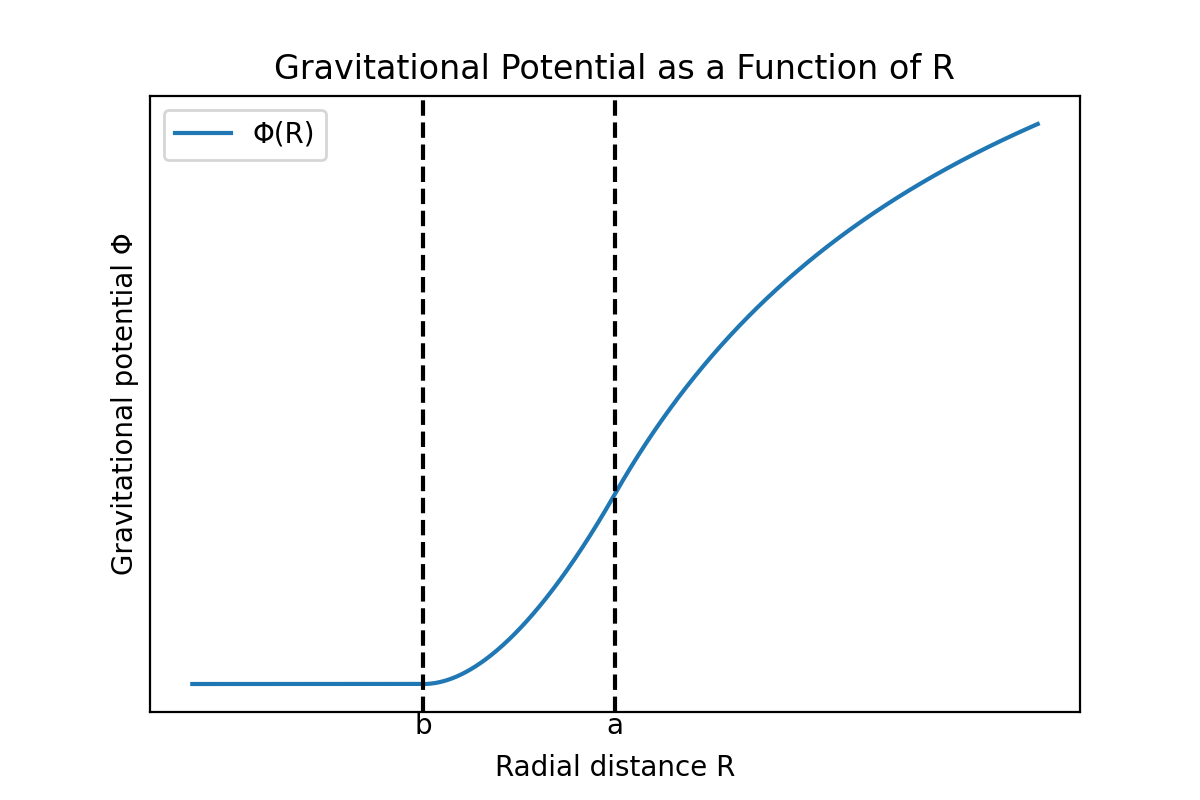
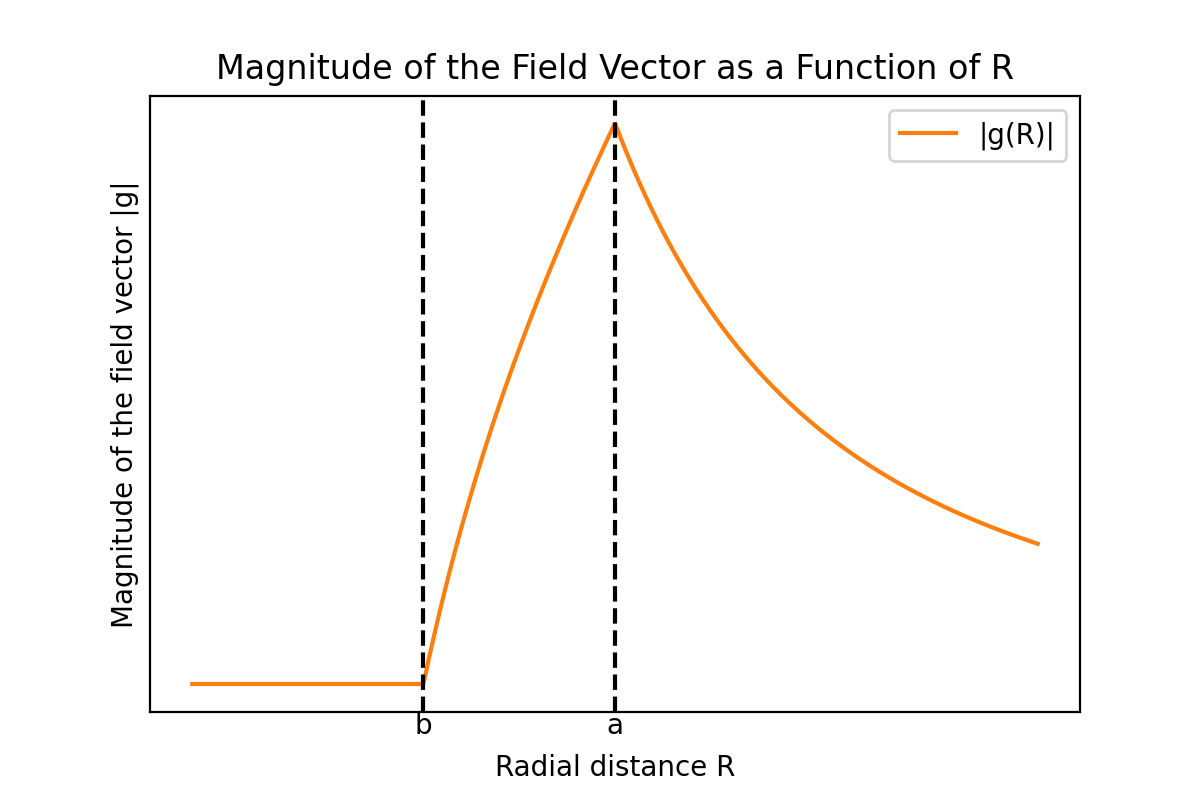
앞서 구한 세 영역에서의 중력 퍼텐셜 $\Phi$, 그리고 그에 따른 중력장 벡터의 크기 $|\mathbf{g}|$를 거리 $R$의 함수로서 그래프로 나타내면 다음과 같다.

• Python 시각화 코드: yunseo-kim/physics-visualization 리포지터리
• 라이선스: See here

중력 퍼텐셜과 중력장 벡터의 크기는 연속적임을 알 수 있다. 만약 중력 퍼텐셜이 어떤 점에서 불연속이면 그 점에서 퍼텐셜의 기울기, 즉 중력의 크기가 그 점에서 무한대가 되는데, 이는 물리적으로 타당하지 않으므로 퍼텐셜 함수는 모든 점에서 연속이어야 한다. 그러나 중력장 벡터의 미분계수는 껍질의 안쪽 면과 바깥쪽 면에서 불연속이다.

예제: 은하 회전 곡선

천문학적 관측에 따르면, 우리은하나 안드로메다 은하와 같이 중심에 대해 회전하는 많은 나선형 은하 속 관측 가능한 질량들은 대부분이 중심부 근처에 집중적으로 분포한다. 그러나 이러한 나선형 은하 속 질량들의 궤도 속력은, 다음 그래프에서 확인할 수 있듯 관측 가능한 질량 분포로부터 이론적으로 예측한 값과 크게 불일치하며 일정 거리 이상에서는 거의 일정하다.

이미지 출처

• 저작자: 위키피디아 유저 PhilHibbs
• 라이선스: Public Domain

나선 은하 M33(삼각형자리 은하)의 회전 곡선

• 저작자: 위키미디어 유저 Mario De Leo
• 라이선스: CC BY-SA 4.0

은하의 질량이 중심부에 집중되어 있을 경우의 거리에 따른 궤도 속력을 예측하여 해당 예측값은 이러한 관측 결과와 일치하지 않음을 확인하고, 은하 중심으로부터 거리 $R$ 이내에 분포하는 질량 $M(R)$이 $R$에 비례하여야 관측 결과를 설명할 수 있음을 보이자.

우선 은하 질량 $M$이 중심부에 집중되어 있을 경우, 거리 $R$에서의 궤도 속력을 구하면 다음과 같다.

\[\frac{GMm}{R^2} = \frac{mv^2}{R}\] \[v = \sqrt{\frac{GM}{R}} \propto \frac{1}{\sqrt{R}}.\]

이 경우 위의 두 그래프에 표시된 점선과 같이 $1/\sqrt{R}$로 감소하는 궤도 속력이 예측되나, 관측 결과에 따르면 궤도 속력 $v$는 거리 $R$과 무관하게 거의 일정하므로 예측과 관측 결과가 일치하지 않는다. 이러한 관측 결과는 $M(R)\propto R$이어야만 설명할 수 있다.

비례 상수 $k$를 써서 $M(R) = kR$로 놓으면,

\[v = \sqrt{\frac{GM(R)}{R}} = \sqrt{Gk}\ \text{(상수)}.\]

이로부터 천체물리학자들은, 많은 은하에는 발견되지 않은 ‘암흑 물질(dark matter)’이 반드시 있고, 이러한 암흑 물질이 우주 질량의 90% 이상을 차지해야 한다는 결론을 내린다. 다만 암흑 물질의 정체는 아직까지 명확히 밝혀지지 않았으며, 주류 이론은 아니지만 암흑 물질의 존재를 가정하지 않고 관측 결과를 설명하려는 수정 뉴턴 역학(Modified Newtonian Dynamics, MOND) 같은 시도도 존재한다. 오늘날 이러한 연구 분야는 천체물리학의 최전선에 맞닿아 있다.