Campo gravitacional e potencial gravitacional

TL;DR

• Lei da gravitação universal de Newton: $\mathbf{F} = -G\cfrac{mM}{r^2}\mathbf{e}_r$
• Para objetos com distribuição contínua de massa e tamanho finito: $\mathbf{F} = -Gm\int_V \cfrac{dM}{r^2}\mathbf{e}_r = -Gm\int_V \cfrac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2} dv^{\prime}$
  • $\rho(\mathbf{r^{\prime}})$: densidade de massa no ponto localizado no vetor posição $\mathbf{r^{\prime}}$ a partir de uma origem arbitrária
  • $dv^{\prime}$: elemento de volume no ponto localizado no vetor posição $\mathbf{r^{\prime}}$ a partir de uma origem arbitrária
• Vetor campo gravitacional:
  • Vetor que representa a força por unidade de massa que uma partícula recebe em um campo criado por um objeto de massa $M$
  • $\mathbf{g} = \cfrac{\mathbf{F}}{m} = - G \cfrac{M}{r^2}\mathbf{e}_r = - G \int_V \cfrac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2}dv^\prime$
  • Tem dimensão de força por unidade de massa ou aceleração
• Potencial gravitacional:
  • $\mathbf{g} \equiv -\nabla \Phi$
  • Tem dimensão de (força por unidade de massa) $\times$ (distância) ou energia por unidade de massa
  • $\Phi = -G\cfrac{M}{r}$
  • Apenas a diferença relativa do potencial gravitacional tem significado, não o valor específico em si
  • Geralmente define-se arbitrariamente a condição $\Phi \to 0$ quando $r \to \infty$ para eliminar a ambiguidade
  • $U = m\Phi, \quad \mathbf{F} = -\nabla U$
• Potencial gravitacional dentro e fora de uma casca esférica (teorema da casca esférica)
  • Quando $R>a$:
    • $\Phi(R>a) = -\cfrac{GM}{R}$
    • Ao calcular o potencial gravitacional em um ponto externo devido a uma distribuição esfericamente simétrica de matéria, pode-se considerar o objeto como uma massa pontual
  • Quando $R<b$:
    • $\Phi(R<b) = -2\pi\rho G(a^2 - b^2)$
    • Dentro de uma casca de massa esfericamente simétrica, o potencial gravitacional é constante independentemente da posição, e a gravidade atuante é $0$
  • Quando $b<R<a$: $\Phi(b<R<a) = -4\pi\rho G \left( \cfrac{a^2}{2} - \cfrac{b^3}{3R} - \cfrac{R^2}{6} \right)$

Campo gravitacional

Lei da gravitação universal de Newton

Newton já havia sistematizado e verificado numericamente a lei da gravitação universal antes de 11666 HE. No entanto, levou mais 20 anos até publicar seus resultados no livro Principia em 11687 HE, porque não conseguia justificar o método de cálculo que assumia a Terra e a Lua como massas pontuais sem tamanho. Felizmente, usando o cálculo que o próprio Newton inventou posteriormente, podemos provar muito mais facilmente esse problema que não era simples para Newton nos anos 1600.

Segundo a lei da gravitação universal de Newton, cada partícula de massa atrai todas as outras partículas no universo com uma força proporcional ao produto das duas massas e inversamente proporcional ao quadrado da distância entre elas. Matematicamente, isso é expresso como:

\[\mathbf{F} = -G\frac{mM}{r^2}\mathbf{e}_r \label{eqn:law_of_gravitation}\tag{1}\]

Fonte da imagem

• Autor: usuário da Wikimedia Dennis Nilsson
• Licença: CC BY 3.0

O vetor unitário $\mathbf{e}_r$ aponta de $M$ para $m$, e o sinal negativo indica que a força é atrativa. Ou seja, $m$ é atraída em direção a $M$.

Experimento de Cavendish

A verificação experimental desta lei e a determinação do valor de $G$ foram realizadas pelo físico inglês Henry Cavendish em 11798 HE. O experimento de Cavendish usa uma balança de torção composta por duas pequenas esferas fixadas nas extremidades de uma haste leve. Essas duas esferas são atraídas em direção a duas outras esferas maiores posicionadas próximas a elas. O valor oficial de $G$ determinado até hoje é $6.673 \pm 0.010 \times 10^{-11} \mathrm{N\cdot m^2/kg^2}$.

Embora $G$ seja uma das constantes fundamentais conhecidas há mais tempo, ela é conhecida com menor precisão do que a maioria das outras constantes fundamentais como $e$, $c$, $\hbar$. Ainda hoje, muitas pesquisas estão sendo realizadas para determinar o valor de $G$ com maior precisão.

Caso de objetos com tamanho finito

A lei da equação ($\ref{eqn:law_of_gravitation}$) pode ser aplicada rigorosamente apenas a partículas pontuais. Se um ou ambos os objetos têm tamanho finito, é necessário fazer a suposição adicional de que o campo gravitacional é um campo linear para calcular a força. Ou seja, assume-se que a força gravitacional total que uma partícula de massa $m$ recebe de várias outras partículas pode ser obtida pela soma vetorial de cada força. Para objetos com distribuição contínua de matéria, a soma é substituída por uma integral:

\[\mathbf{F} = -Gm\int_V \frac{dM}{r^2}\mathbf{e}_r = -Gm\int_V \frac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2} dv^{\prime} \label{eqn:integral_form}\tag{2}\]

• $\rho(\mathbf{r^{\prime}})$: densidade de massa no ponto localizado no vetor posição $\mathbf{r^{\prime}}$ a partir de uma origem arbitrária
• $dv^{\prime}$: elemento de volume no ponto localizado no vetor posição $\mathbf{r^{\prime}}$ a partir de uma origem arbitrária

Se tanto o objeto de massa $M$ quanto o objeto de massa $m$ têm tamanho finito, uma segunda integral de volume sobre $m$ também é necessária para obter a força gravitacional total.

Vetor campo gravitacional

O vetor campo gravitacional $\mathbf{g}$ é definido como o vetor que representa a força por unidade de massa que uma partícula recebe em um campo criado por um objeto de massa $M$:

\[\mathbf{g} = \frac{\mathbf{F}}{m} = - G \frac{M}{r^2}\mathbf{e}_r \label{eqn:g_vector}\tag{3}\]

ou

\[\boxed{\mathbf{g} = - G \int_V \frac{\rho(\mathbf{r^\prime})\mathbf{e}_r}{r^2}dv^\prime} \tag{4}\]

Aqui, a direção de $\mathbf{e}_r$ varia conforme $\mathbf{r^\prime}$.

Esta quantidade $\mathbf{g}$ tem dimensão de força por unidade de massa ou aceleração. A magnitude do vetor campo gravitacional $\mathbf{g}$ próximo à superfície da Terra é igual à quantidade que chamamos de constante de aceleração gravitacional, com $|\mathbf{g}| \approx 9.80\mathrm{m/s^2}$.

Potencial gravitacional

Definição

O vetor campo gravitacional $\mathbf{g}$ varia como $1/r^2$ e, portanto, satisfaz a condição ($\nabla \times \mathbf{g} \equiv 0$) para ser expresso como o gradiente de alguma função escalar (potencial). Assim, podemos escrever:

\[\mathbf{g} \equiv -\nabla \Phi \label{eqn:gradient_phi}\tag{5}\]

onde $\Phi$ é chamado de potencial gravitacional e tem dimensão de (força por unidade de massa) $\times$ (distância) ou energia por unidade de massa.

Como $\mathbf{g}$ depende apenas do raio, $\Phi$ também varia com $r$. Das equações ($\ref{eqn:g_vector}$) e ($\ref{eqn:gradient_phi}$):

\[\nabla\Phi = \frac{d\Phi}{dr}\mathbf{e}_r = G\frac{M}{r^2}\mathbf{e}_r\]

Integrando isso, obtemos:

\[\boxed{\Phi = -G\frac{M}{r}} \label{eqn:g_potential}\tag{6}\]

Como apenas a diferença relativa do potencial gravitacional tem significado, não a magnitude do valor absoluto, a constante de integração pode ser omitida. Geralmente define-se arbitrariamente a condição $\Phi \to 0$ quando $r \to \infty$ para eliminar a ambiguidade, e a equação ($\ref{eqn:g_potential}$) também satisfaz esta condição.

Para distribuições contínuas de matéria, o potencial gravitacional é:

\[\Phi = -G\int_V \frac{\rho(\mathbf{r\prime})}{r}dv^\prime \label{eqn:g_potential_v}\tag{7}\]

Para distribuições superficiais de massa em cascas finas:

\[\Phi = -G\int_S \frac{\rho_s}{r}da^\prime. \label{eqn:g_potential_s}\tag{8}\]

E para fontes de massa lineares com densidade linear $\rho_l$:

\[\Phi = -G\int_\Gamma \frac{\rho_l}{r}ds^\prime. \label{eqn:g_potential_l}\tag{9}\]

Significado físico

Considere o trabalho por unidade de massa $dW^\prime$ que um objeto realiza quando se move $d\mathbf{r}$ em um campo gravitacional.

\[\begin{align*} dW^\prime &= -\mathbf{g}\cdot d\mathbf{r} = (\nabla \Phi)\cdot d\mathbf{r} \\ &= \sum_i \frac{\partial \Phi}{\partial x_i}dx_i = d\Phi \label{eqn:work}\tag{10} \end{align*}\]

Nesta equação, $\Phi$ é uma função apenas das coordenadas de posição, expressa como $\Phi=\Phi(x_1, x_2, x_3) = \Phi(x_i)$. Portanto, o trabalho por unidade de massa que um objeto realiza ao se mover de um ponto a outro em um campo gravitacional é igual à diferença de potencial entre esses dois pontos.

Se definirmos o potencial gravitacional no infinito como $0$, então $\Phi$ em qualquer ponto pode ser interpretado como o trabalho por unidade de massa necessário para mover o objeto do infinito até esse ponto. A energia potencial do objeto é igual ao produto de sua massa e o potencial gravitacional $\Phi$, então se $U$ é a energia potencial:

\[U = m\Phi. \label{eqn:potential_e}\tag{11}\]

Portanto, a força gravitacional que atua sobre o objeto é obtida aplicando um sinal negativo ao gradiente de sua energia potencial.

\[\mathbf{F} = -\nabla U \label{eqn:force_and_potential}\tag{12}\]

Quando um objeto está em um campo gravitacional criado por alguma massa, sempre existe alguma energia potencial. Esta energia potencial está rigorosamente no próprio campo, mas convencionalmente é expressa como a energia potencial do objeto.

Exemplo: Potencial gravitacional dentro e fora de uma casca esférica (teorema da casca esférica)

Configuração de coordenadas e expressão do potencial gravitacional como integral

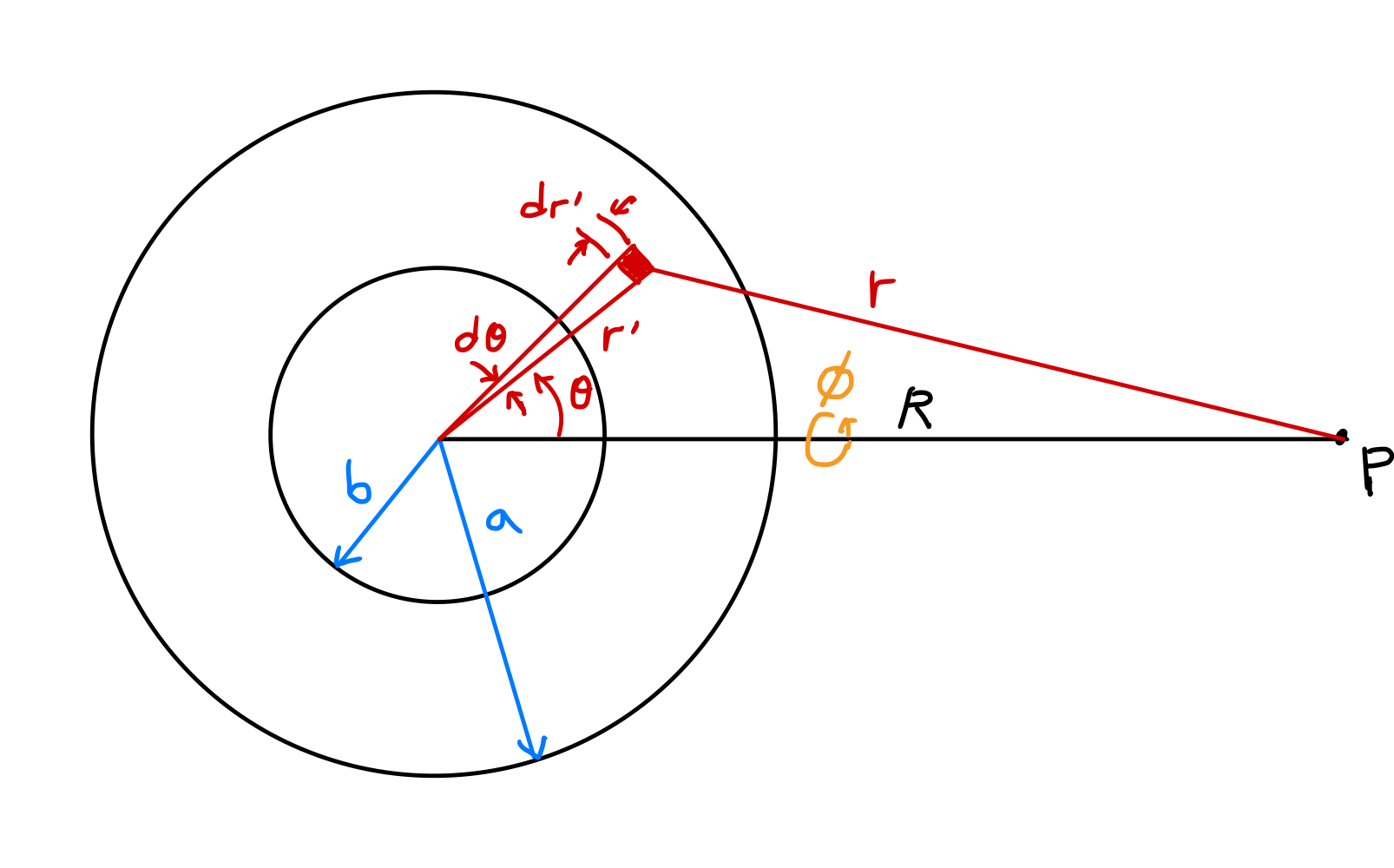
Vamos encontrar o potencial gravitacional dentro e fora de uma casca esférica uniforme com raio interno $b$ e raio externo $a$. Embora a gravidade devido à casca esférica possa ser obtida calculando diretamente os componentes da força que atuam sobre uma massa unitária no campo, usar o método do potencial é mais simples.

Na figura acima, vamos calcular o potencial no ponto $P$ a uma distância $R$ do centro. Assumindo distribuição uniforme de massa na casca, $\rho(r^\prime)=\rho$, e como há simetria em relação ao ângulo azimutal $\phi$ com base na linha que conecta o centro da esfera ao ponto $P$:

\[\begin{align*} \Phi &= -G\int_V \frac{\rho(r^\prime)}{r}dv^\prime \\ &= -\rho G \int_0^{2\pi} \int_0^\pi \int_b^a \frac{1}{r}(dr^\prime)(r^\prime d\theta)(r^\prime \sin\theta\, d\phi) \\ &= -\rho G \int_0^{2\pi} d\phi \int_b^a {r^\prime}^2 dr^\prime \int_0^\pi \frac{\sin\theta}{r}d\theta \\ &= -2\pi\rho G \int_b^a {r^\prime}^2 dr^\prime \int_0^\pi \frac{\sin\theta}{r}d\theta. \label{eqn:spherical_shell_1}\tag{13} \end{align*}\]

Pela lei dos cossenos:

\[r^2 = {r^\prime}^2 + R^2 - 2r^\prime R \cos\theta \label{eqn:law_of_cosines}\tag{14}\]

Como $R$ é constante, diferenciando esta equação em relação a $r^\prime$:

\[2rdr = 2r^\prime R \sin\theta d\theta\] \[\frac{\sin\theta}{r}d\theta = \frac{dr}{r^\prime R} \tag{15}\]

Substituindo isso na equação ($\ref{eqn:spherical_shell_1}$):

\[\Phi = -\frac{2\pi\rho G}{R} \int_b^a r^\prime dr^\prime \int_{r_\mathrm{min}}^{r_\mathrm{max}} dr. \label{eqn:spherical_shell_2}\tag{16}\]

Aqui, $r_\mathrm{max}$ e $r_\mathrm{min}$ são determinados pela posição do ponto $P$.

Quando $R>a$

\(\begin{align*} \Phi(R>a) &= -\frac{2\pi\rho G}{R} \int_b^a r^\prime dr^\prime \int_{R-r^\prime}^{R+r^\prime} dr \\ &= - \frac{4\pi\rho G}{R} \int_b^a {r^\prime}^2 dr^\prime \\ &= - \frac{4}{3}\frac{\pi\rho G}{R}(a^3 - b^3). \label{eqn:spherical_shell_outside_1}\tag{17} \end{align*}\)

A massa $M$ da casca esférica é:

\[M = \frac{4}{3}\pi\rho(a^3 - b^3) \label{eqn:mass_of_shell}\tag{18}\]

Portanto, o potencial é:

\[\boxed{\Phi(R>a) = -\frac{GM}{R}} \label{eqn:spherical_shell_outside_2}\tag{19}\]

Comparando o potencial gravitacional devido a uma massa pontual de massa $M$ na equação ($\ref{eqn:g_potential}$) com o resultado que acabamos de obter ($\ref{eqn:spherical_shell_outside_2}$), vemos que são idênticos. Isso significa que ao calcular o potencial gravitacional em um ponto externo devido a uma distribuição esfericamente simétrica de matéria, podemos considerar toda a massa como concentrada no centro. A maioria dos corpos celestes esféricos de tamanho considerável, como a Terra ou a Lua, se enquadra nesta categoria, pois podem ser considerados como inúmeras cascas esféricas concêntricas com diferentes diâmetros sobrepostas como uma matryoshka. Isso fornece a base válida para assumir corpos celestes como a Terra ou a Lua como massas pontuais sem tamanho nos cálculos mencionada no início deste artigo.

Quando $R<b$

\(\begin{align*} \Phi(R<b) &= -\frac{2\pi\rho G}{R} \int_b^a r^\prime dr^\prime \int_{r^\prime - R}^{r^\prime + R}dr \\ &= -4\pi\rho G \int_b^a r^\prime dr^\prime \\ &= -2\pi\rho G(a^2 - b^2). \label{eqn:spherical_shell_inside}\tag{20} \end{align*}\)

Dentro de uma casca de massa esfericamente simétrica, o potencial gravitacional é constante independentemente da posição, e a gravidade atuante é $0$.

Isso também é uma das principais evidências de que a “teoria da Terra oca”, uma das pseudociências representativas, é absurda. Se a Terra fosse uma casca esférica com interior vazio, como afirma a teoria da Terra oca, a gravidade terrestre não atuaria sobre todos os objetos dentro dessa cavidade. Considerando a massa e o volume da Terra, não pode haver uma cavidade terrestre, e mesmo que houvesse, os seres vivos lá não viveriam usando o interior da casca esférica como solo, mas flutuariam em estado de ausência de peso como em uma estação espacial.
Embora microrganismos possam viver em camadas profundas a alguns quilômetros subterrâneos, pelo menos não é possível da forma que a teoria da Terra oca afirma. Eu também gosto muito do romance de Júlio Verne “Viagem ao Centro da Terra” e do filme “Jornada ao Centro da Terra”, mas devemos apreciar as obras de ficção como ficção e não levá-las a sério.

Quando $b<R<a$

\(\begin{align*} \Phi(b<R<a) &= -\frac{4\pi\rho G}{3R}(R^3 - b^3) - 2\pi\rho G(a^2 - R^2) \\ &= -4\pi\rho G \left( \frac{a^2}{2} - \frac{b^3}{3R} - \frac{R^2}{6} \right) \label{eqn:within_spherical_shell}\tag{21} \end{align*}\)

Resultados

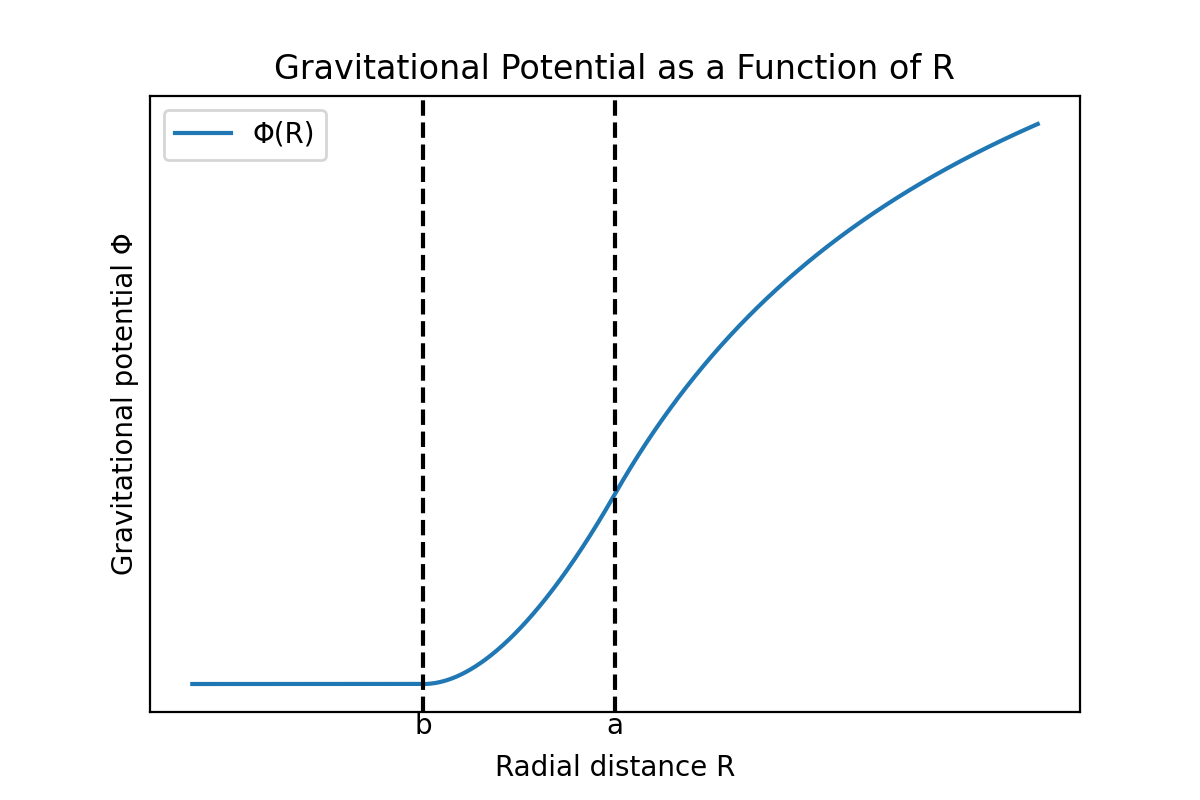
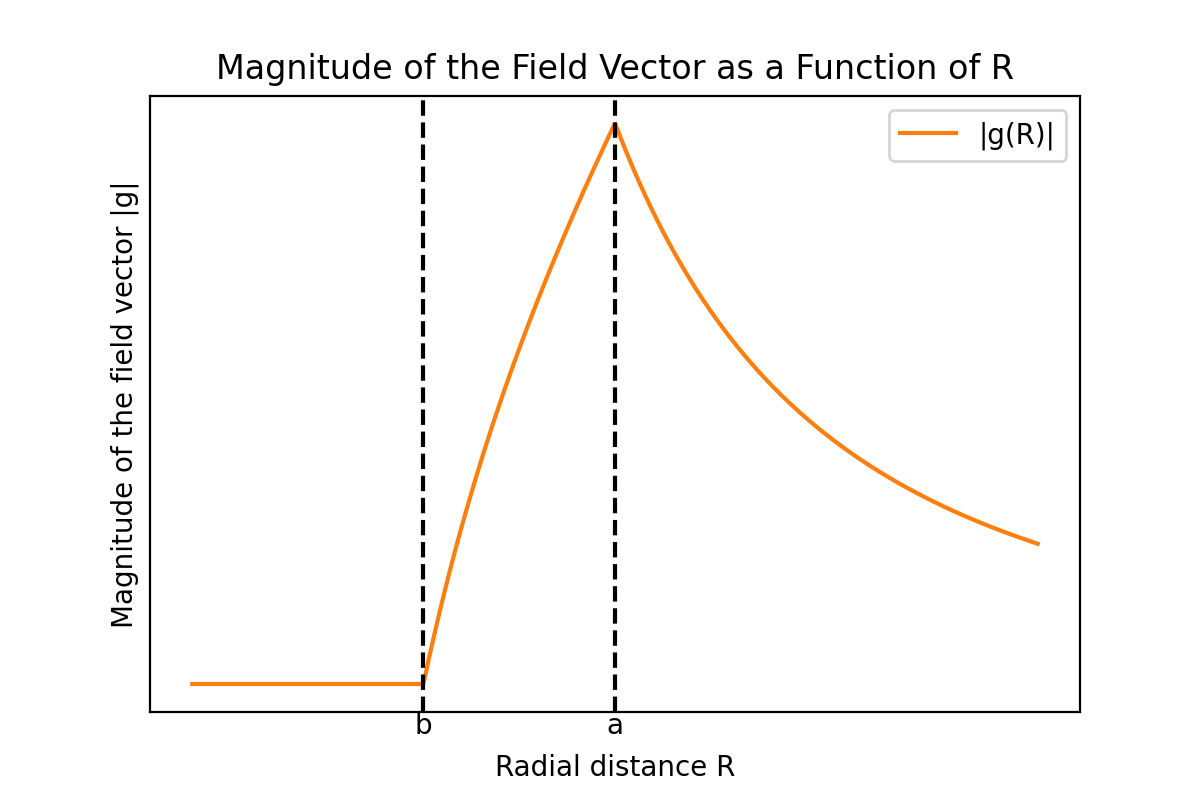
O potencial gravitacional $\Phi$ nas três regiões calculadas anteriormente e a magnitude correspondente do vetor campo gravitacional $|\mathbf{g}|$ como função da distância $R$ são mostrados nos gráficos a seguir.

• Código de visualização Python: repositório yunseo-kim/physics-visualizations
• Licença: Ver aqui

Pode-se ver que o potencial gravitacional e a magnitude do vetor campo gravitacional são contínuos. Se o potencial gravitacional fosse descontínuo em algum ponto, o gradiente do potencial nesse ponto, ou seja, a magnitude da gravidade, se tornaria infinita nesse ponto, o que não é fisicamente válido, então a função potencial deve ser contínua em todos os pontos. No entanto, a derivada do vetor campo gravitacional é descontínua nas superfícies interna e externa da casca.

Exemplo: Curvas de rotação galácticas

Segundo observações astronômicas, em muitas galáxias espirais que rotam em torno do centro, como a Via Láctea ou a galáxia de Andrômeda, a maioria das massas observáveis está concentrada próximo ao centro. No entanto, as velocidades orbitais das massas nessas galáxias espirais diferem significativamente dos valores teoricamente previstos a partir da distribuição de massa observável, como pode ser confirmado no gráfico a seguir, e são quase constantes além de uma certa distância.

Fonte da imagem

• Autor: usuário da Wikipedia PhilHibbs
• Licença: Domínio Público

Curva de rotação da galáxia espiral M33 (galáxia do Triângulo)

• Autor: usuário da Wikimedia Mario De Leo
• Licença: CC BY-SA 4.0

Vamos prever a velocidade orbital em função da distância quando a massa da galáxia está concentrada no centro, confirmar que essa previsão não coincide com os resultados observacionais, e mostrar que a massa $M(R)$ distribuída dentro da distância $R$ do centro galáctico deve ser proporcional a $R$ para explicar os resultados observacionais.

Primeiro, quando a massa galáctica $M$ está concentrada no centro, a velocidade orbital à distância $R$ é:

\[\frac{GMm}{R^2} = \frac{mv^2}{R}\] \[v = \sqrt{\frac{GM}{R}} \propto \frac{1}{\sqrt{R}}.\]

Neste caso, prevê-se uma velocidade orbital que diminui como $1/\sqrt{R}$, como mostrado pelas linhas pontilhadas nos dois gráficos acima, mas segundo os resultados observacionais, a velocidade orbital $v$ é quase constante independentemente da distância $R$, então a previsão e os resultados observacionais não coincidem. Esses resultados observacionais só podem ser explicados se $M(R)\propto R$.

Definindo $M(R) = kR$ usando a constante de proporcionalidade $k$:

\[v = \sqrt{\frac{GM(R)}{R}} = \sqrt{Gk}\ \text{(constante)}.\]

A partir disso, os astrofísicos concluem que deve haver ‘matéria escura’ não descoberta em muitas galáxias, e que essa matéria escura deve constituir mais de 90% da massa do universo. No entanto, a identidade da matéria escura ainda não foi claramente revelada, e embora não seja a teoria principal, existem tentativas como a Dinâmica Newtoniana Modificada (MOND) que tentam explicar os resultados observacionais sem assumir a existência de matéria escura. Hoje, esses campos de pesquisa estão na vanguarda da astrofísica.